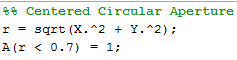Cellular Automata(CA) Project: Forest Fire

Welcome, reader(Dr. Bantang or someone who, for some reason, stumbled upon my blog)! For this post, I wish to document my experience in coding from scratch a simple cellular automata algorithm that models a forest fire.

Cellular automata systems are composed of cells that can be in multiple states depending on the system of choice. These cells can change state according to a set of simple rules. Using these simple, and often local, rules, complex phenomena from the real world may be modeled.

Forest Fire CA description

In this section, I describe the CA algorithm used to model a forest fire.

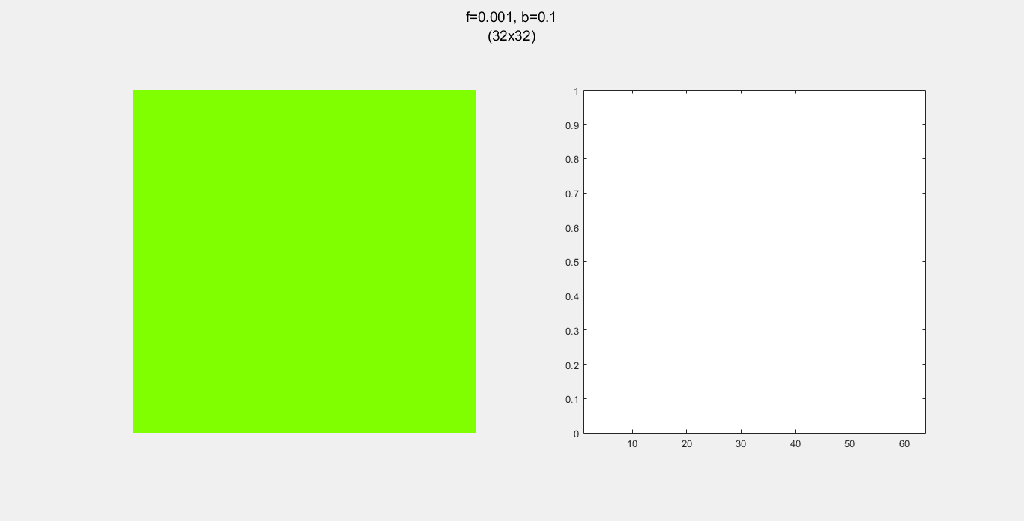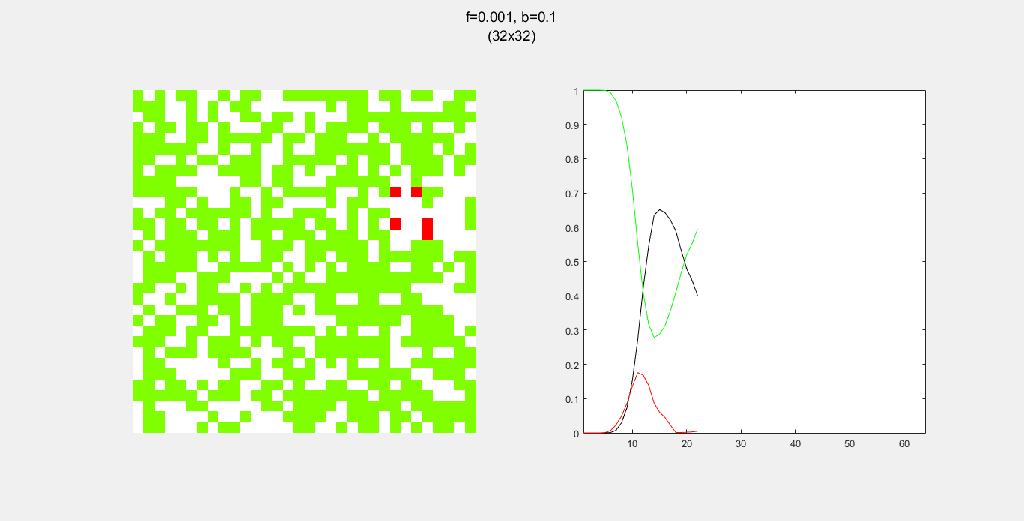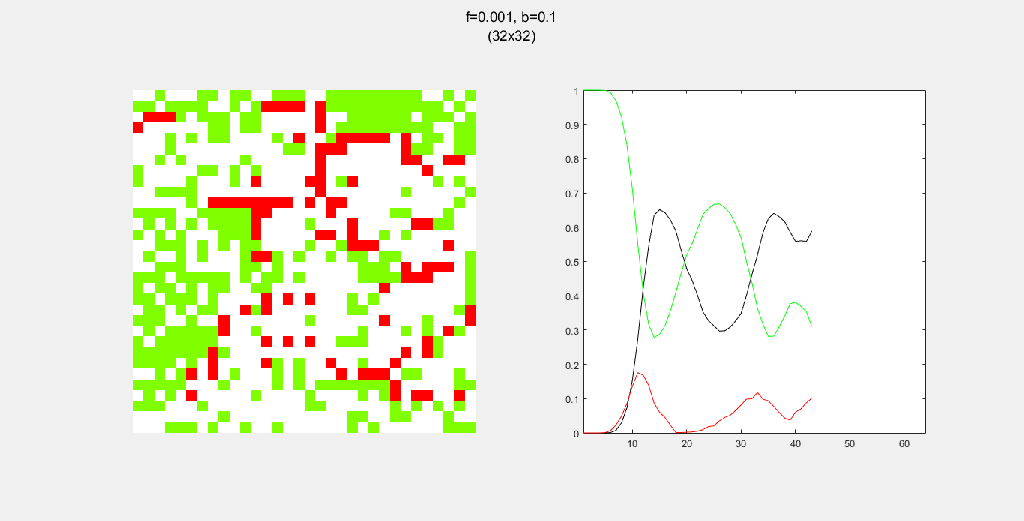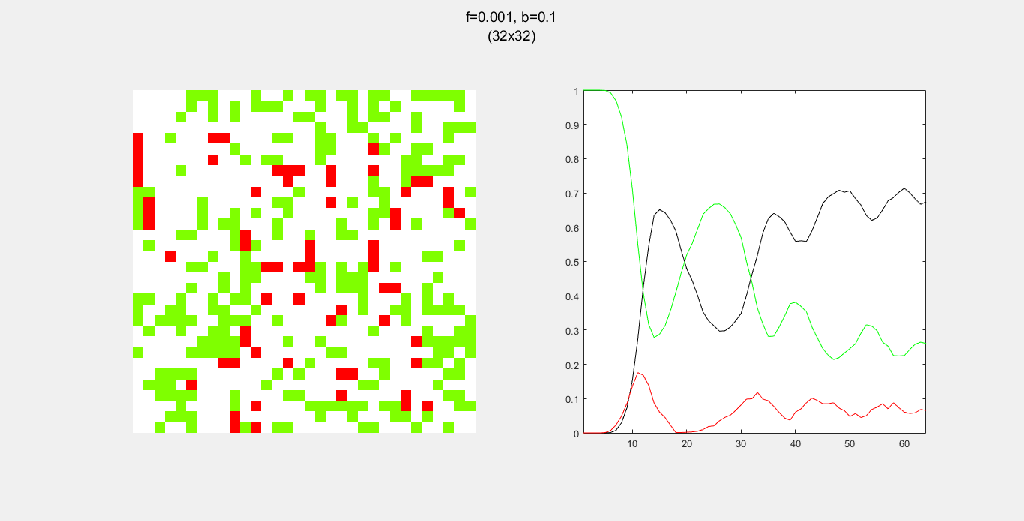
The forest is modeled as an NxN 2D grid, where each cell can be in any of 3 states: (1) empty land, (2) green tree or (3) burning tree.

The states of the cell are updated per time step based on the following 4 rules.

1. A burning tree becomes empty land at the next time step.
2. Green trees near a burning tree become burning trees at the next time step.
3. A green tree spontaneously combusts into a burning tree with probability f(fire).
4. Empty land instantly grows a green tree with probability b(birth)

Forest Fire examples

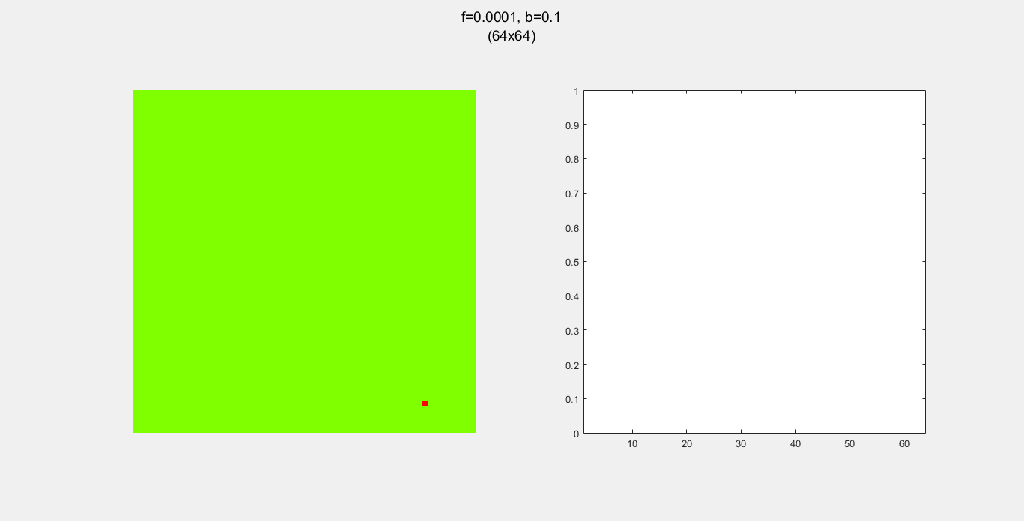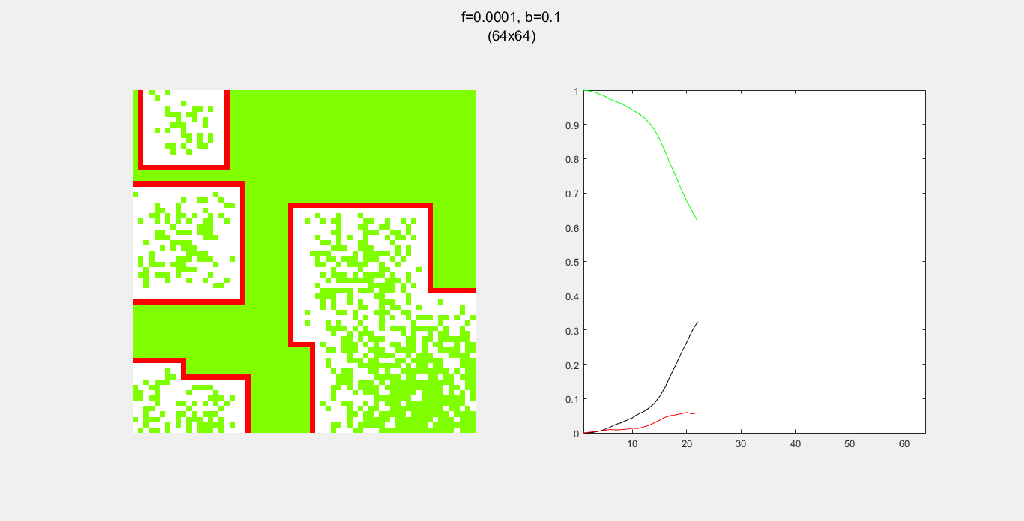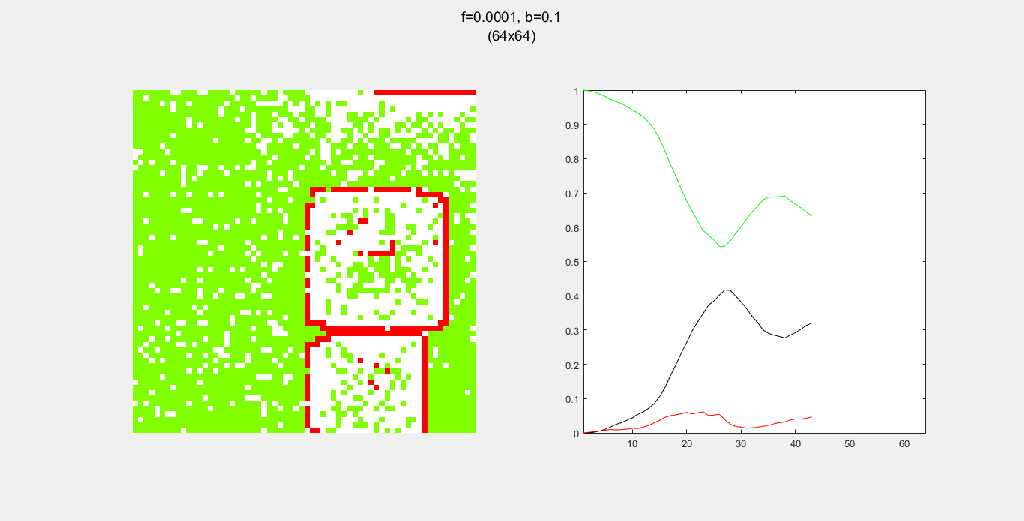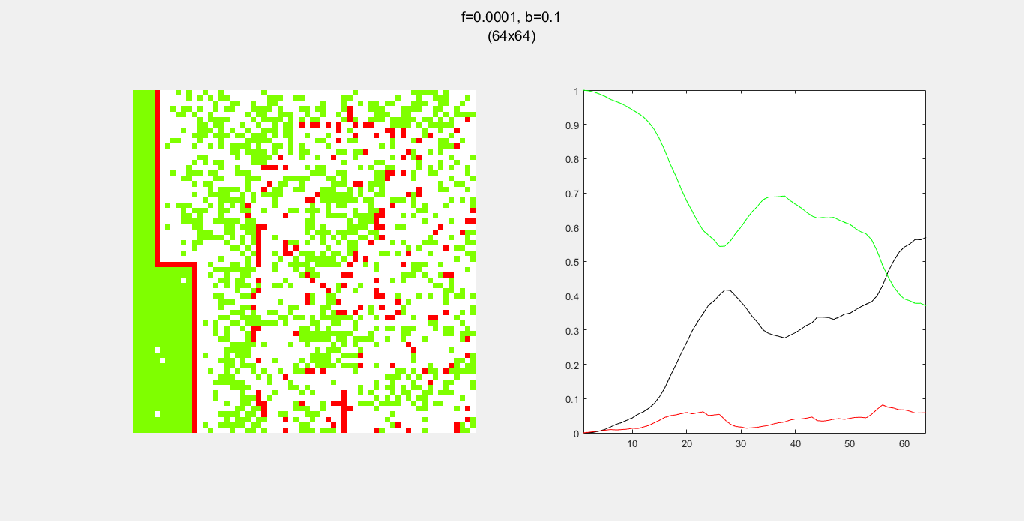
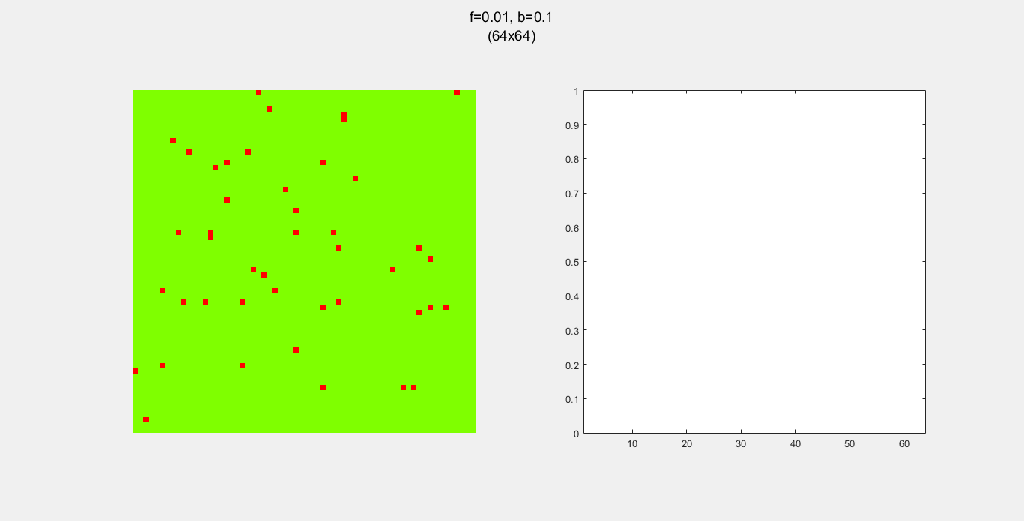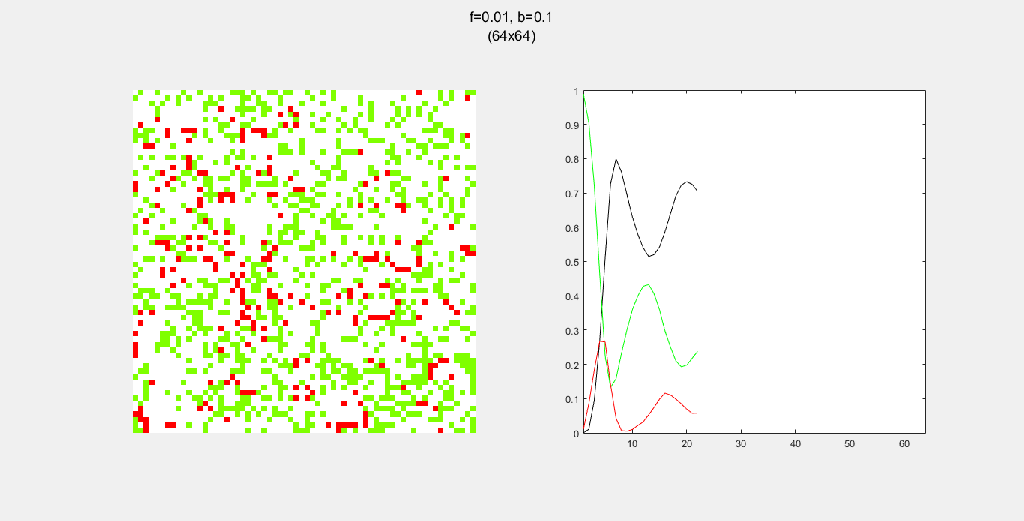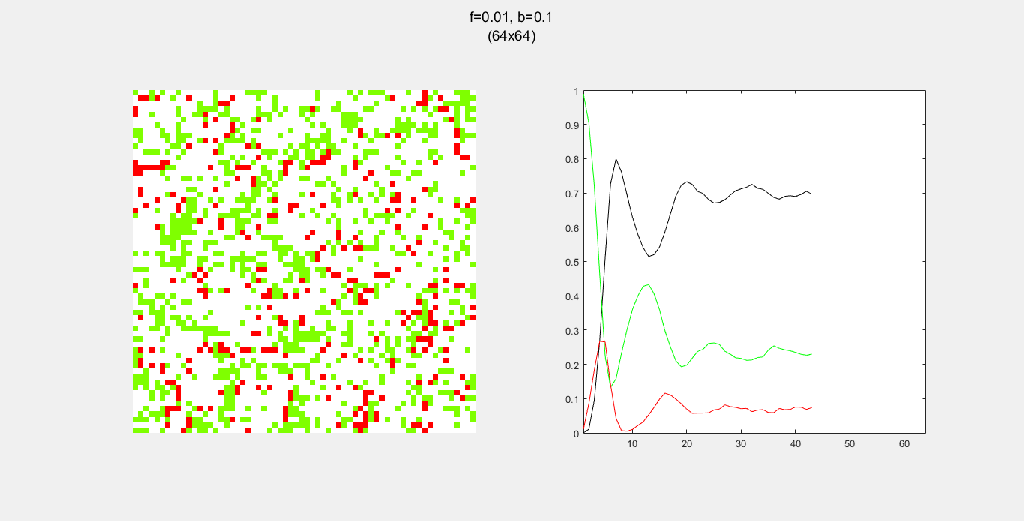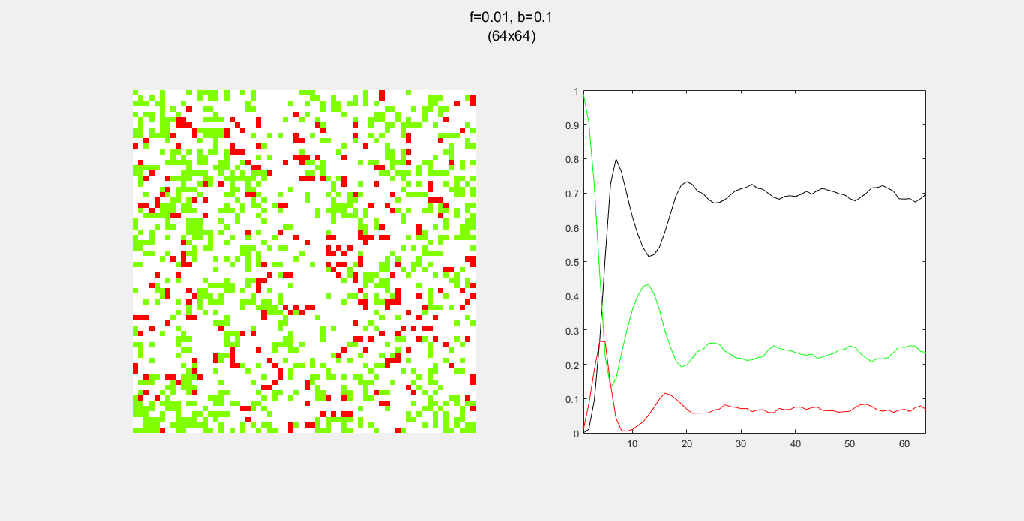
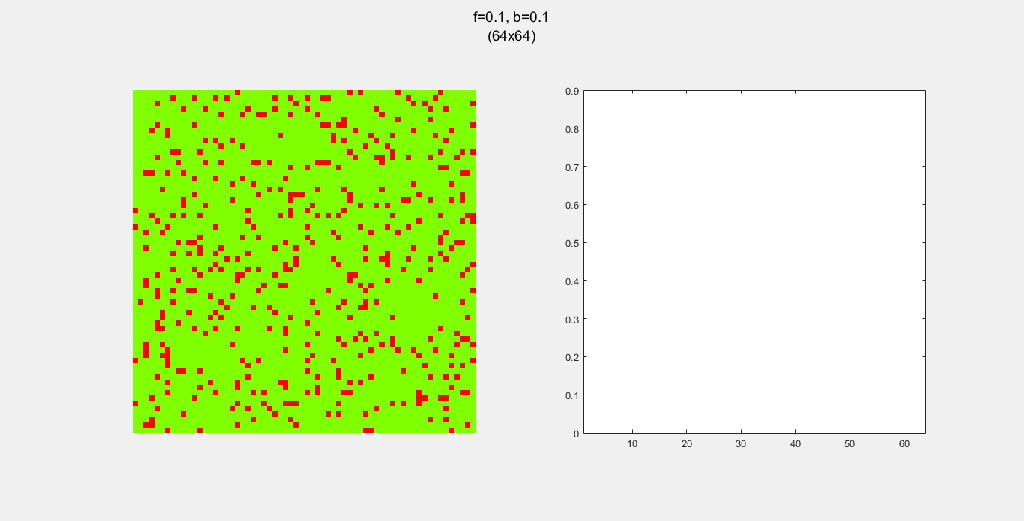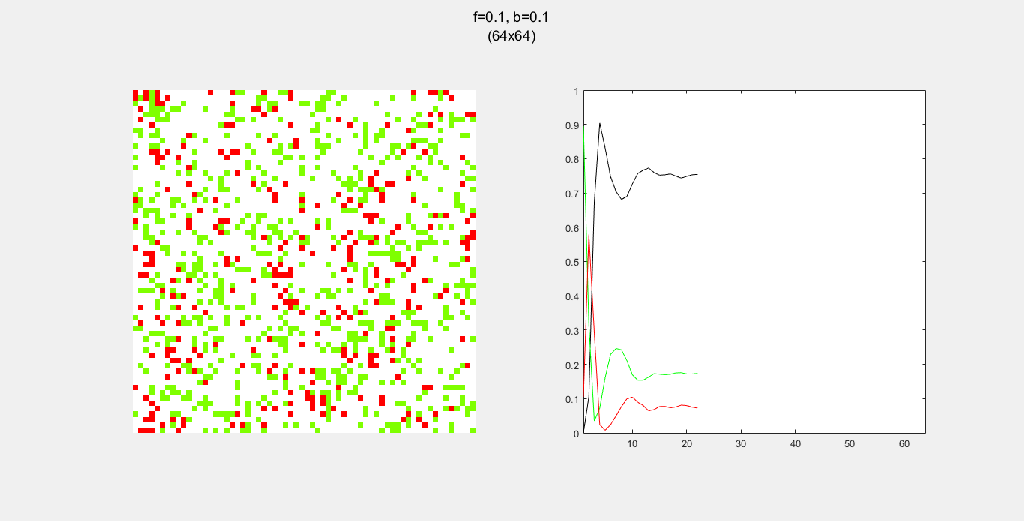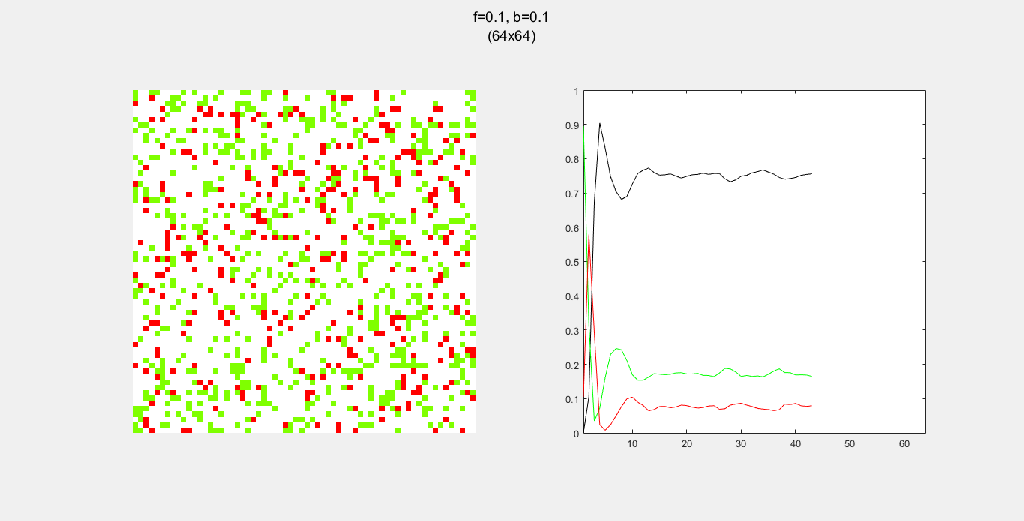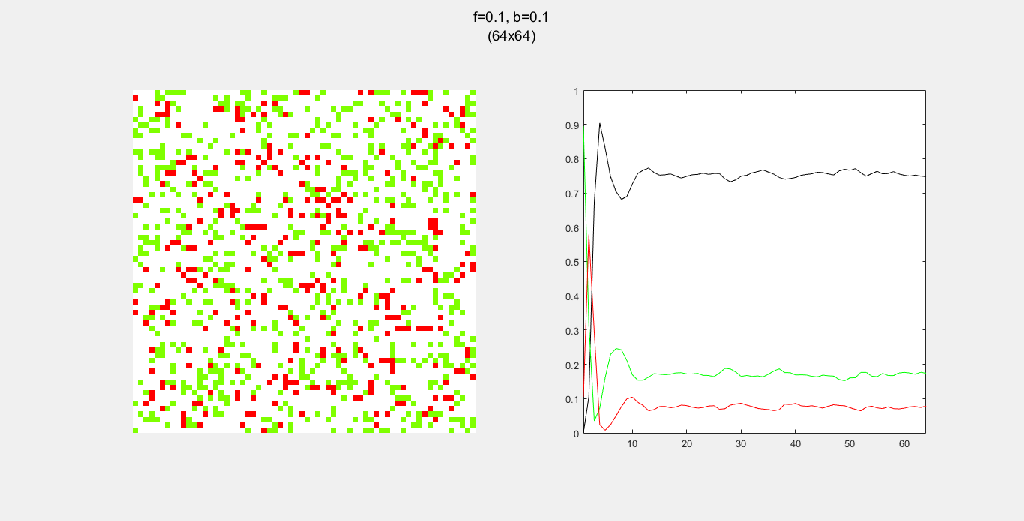
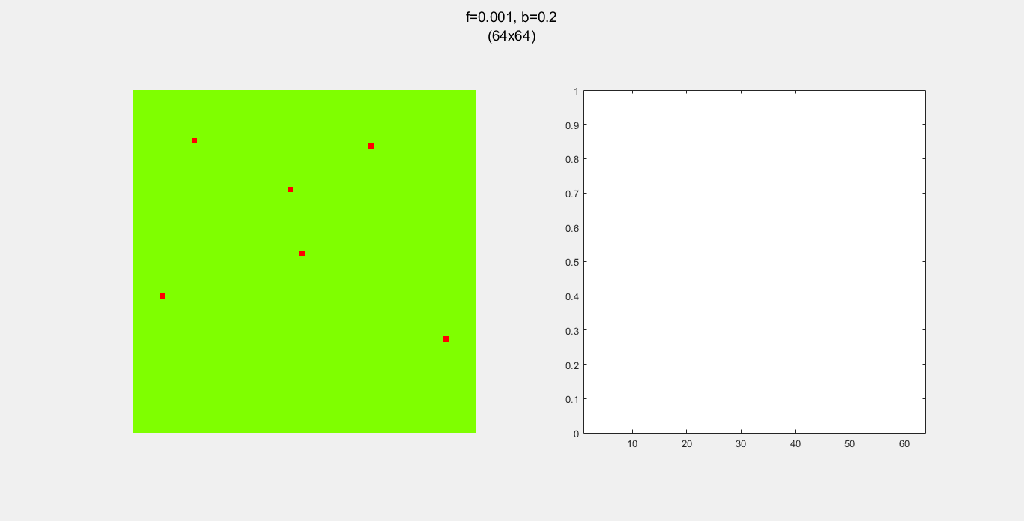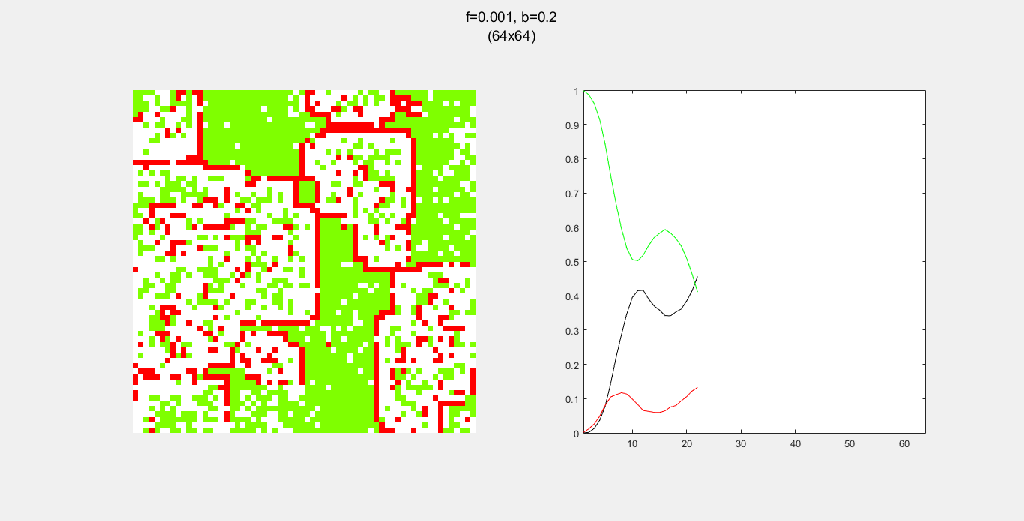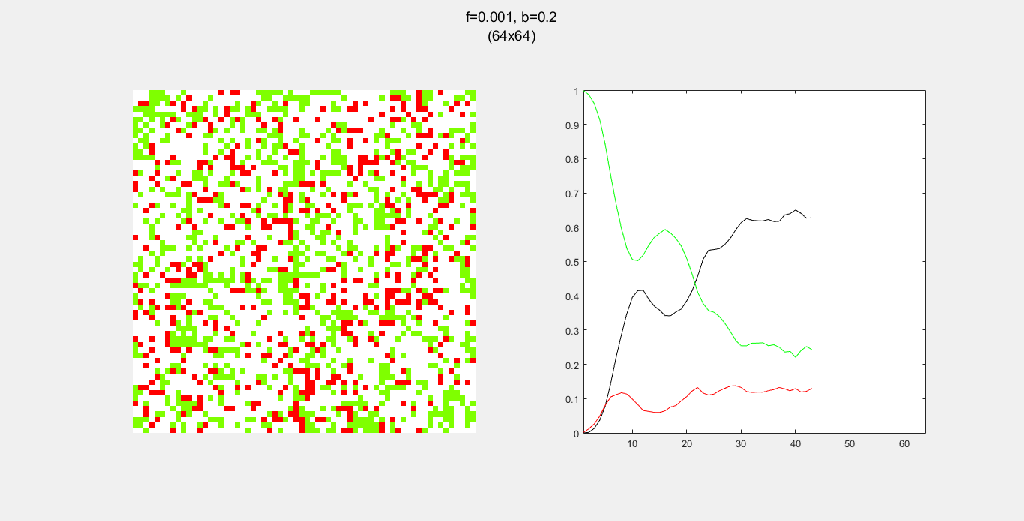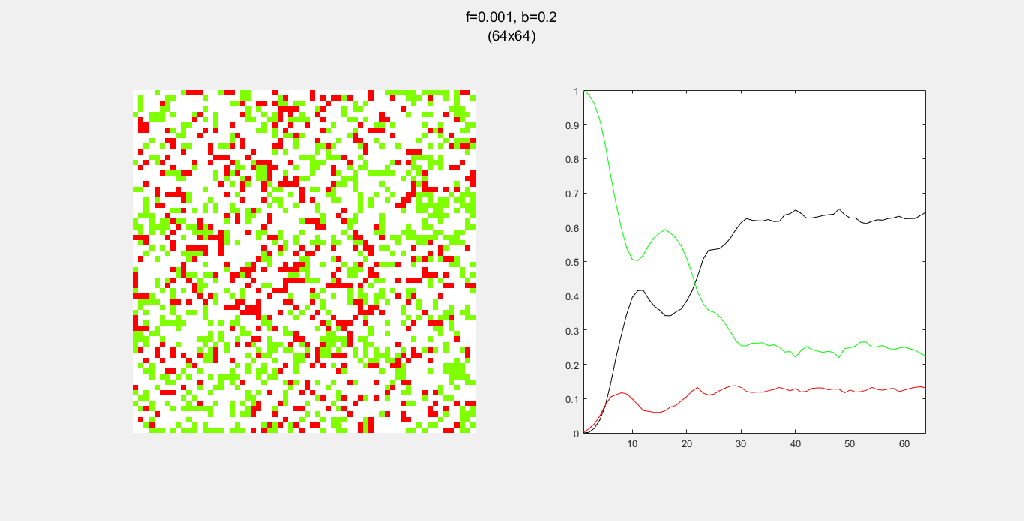
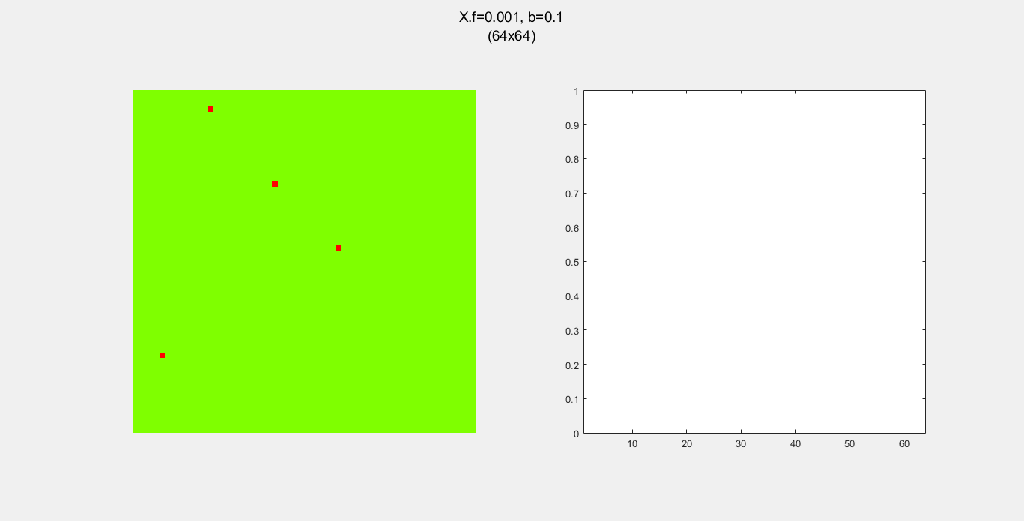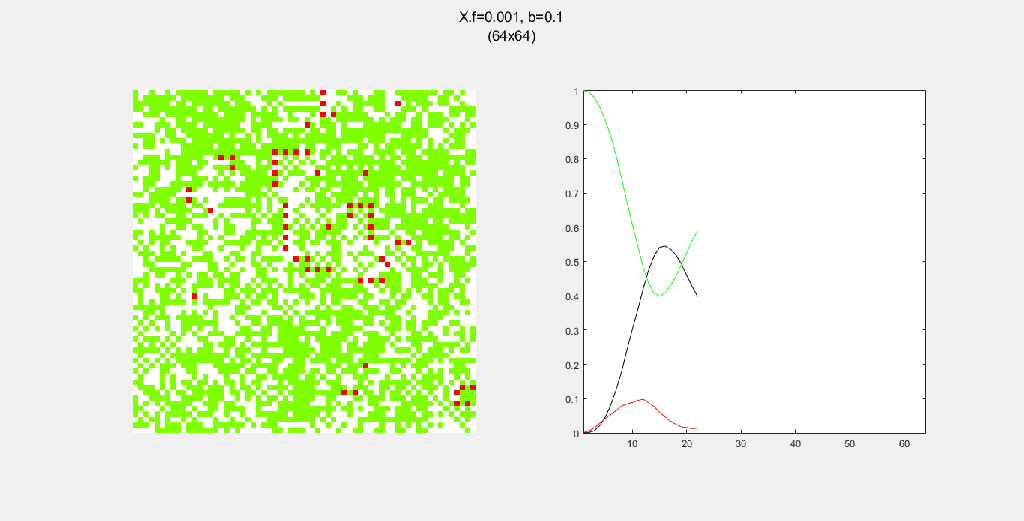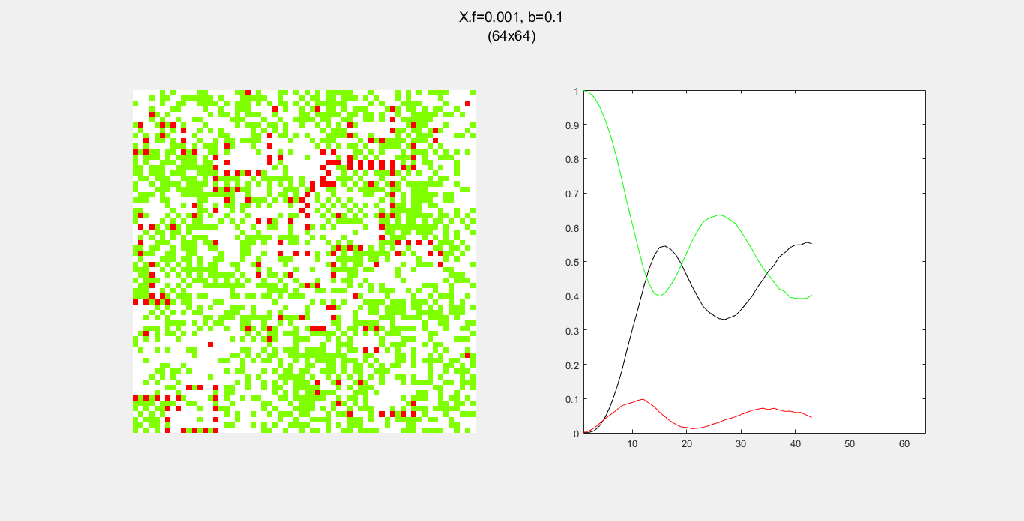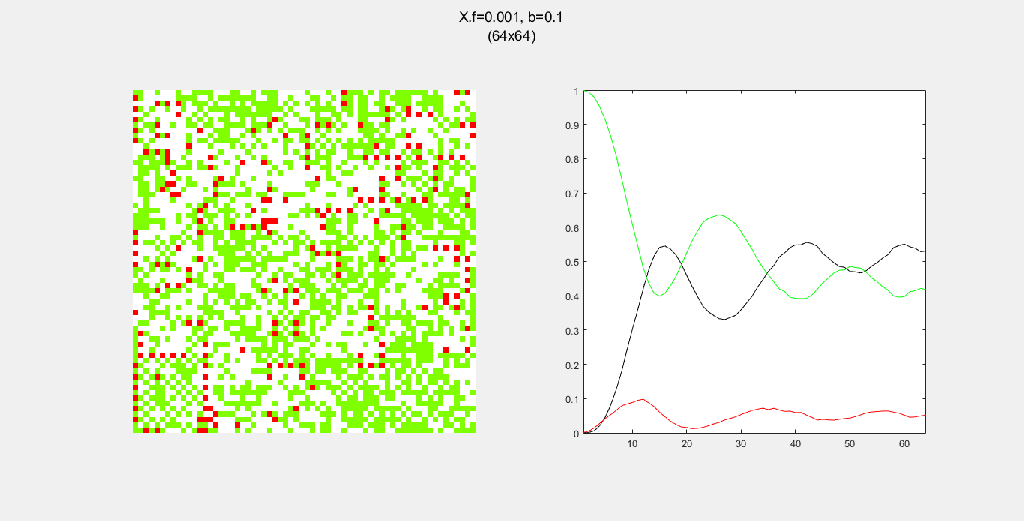
Here are some examples of the forest fire system. I mostly played around with (1) N, the size of the forest, (2) spread pattern, which governs how fire spreads from a burning tree to nearby green trees, (3) f, the probability of spontaneous combustion, and (4) b, the probability of “tree birth”.

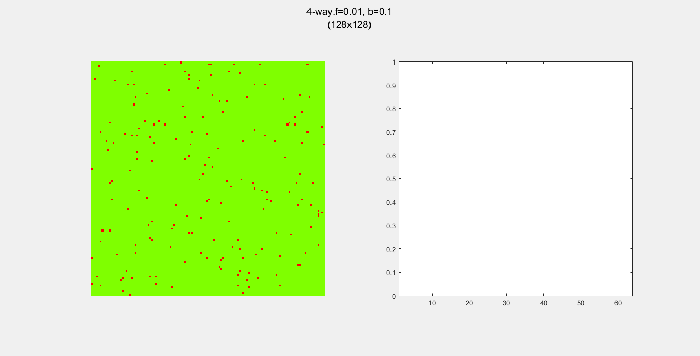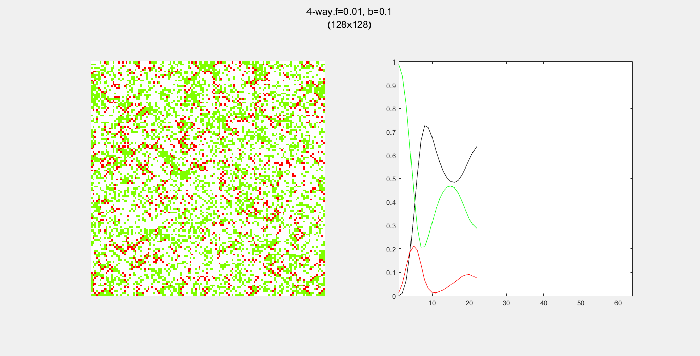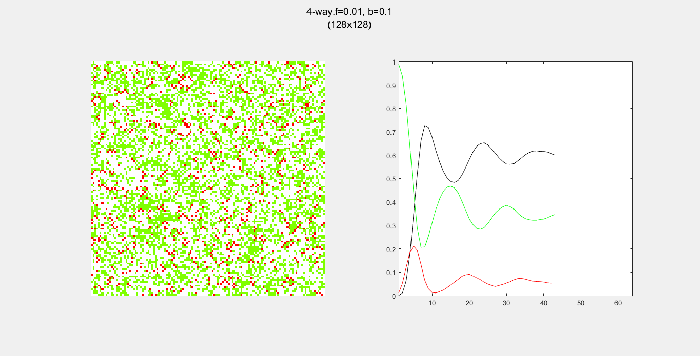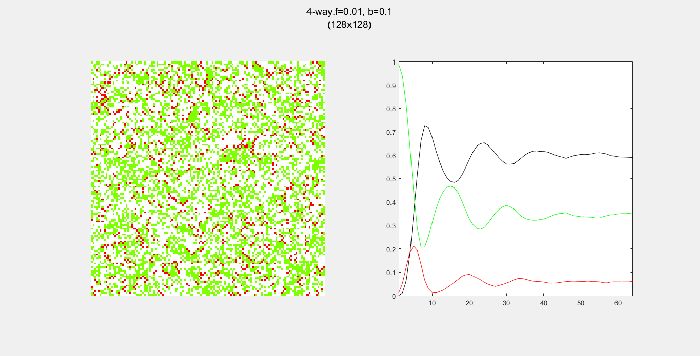
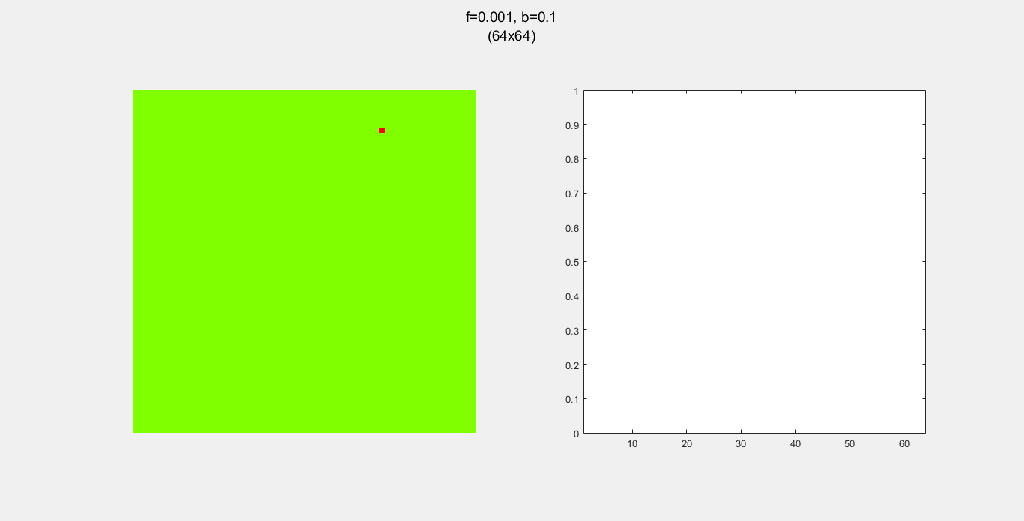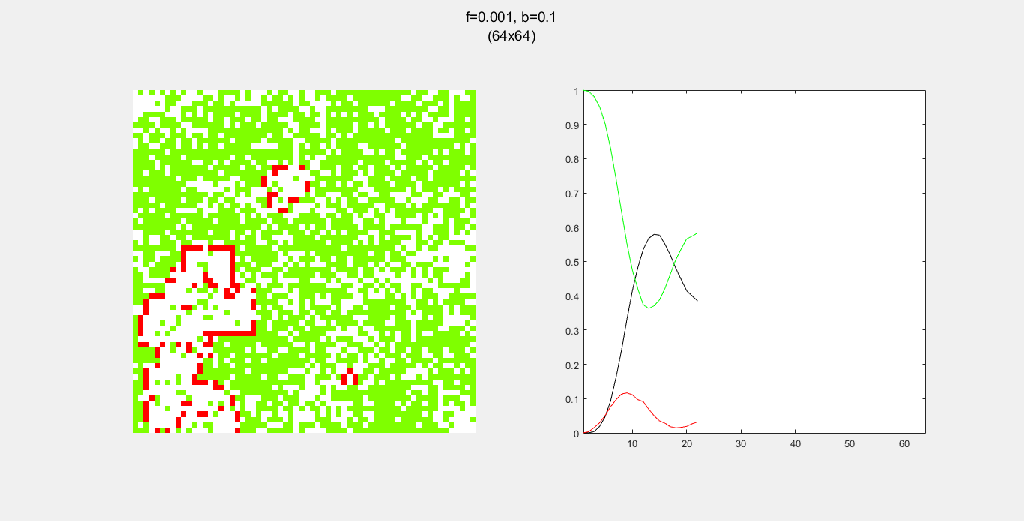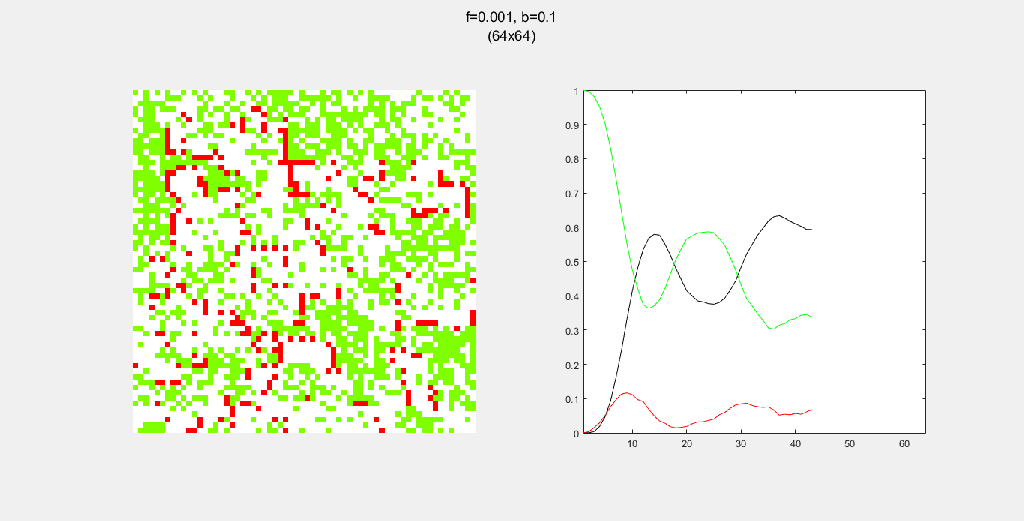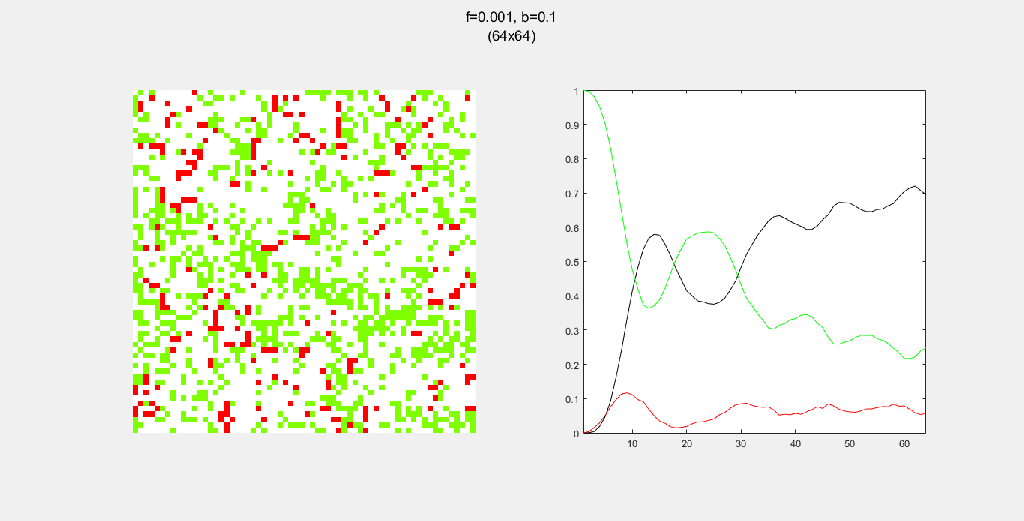
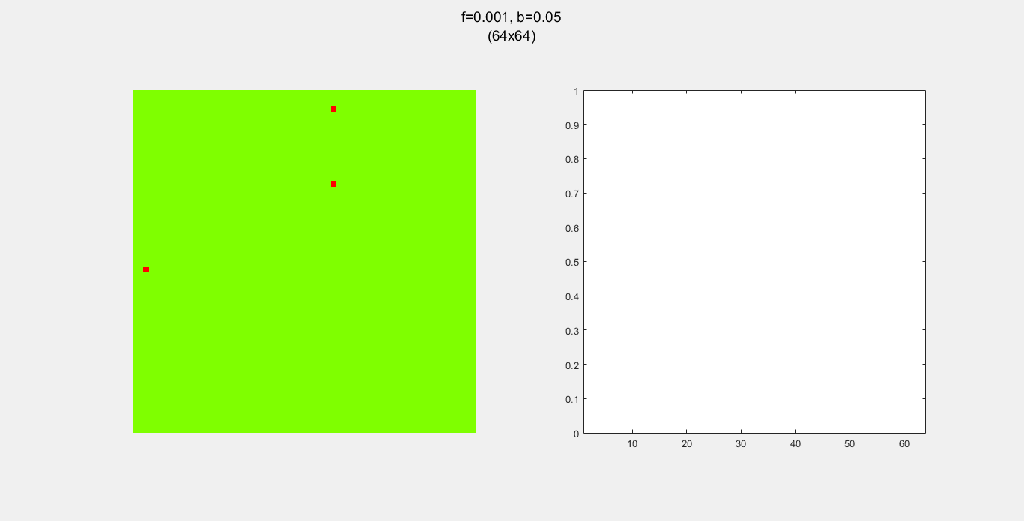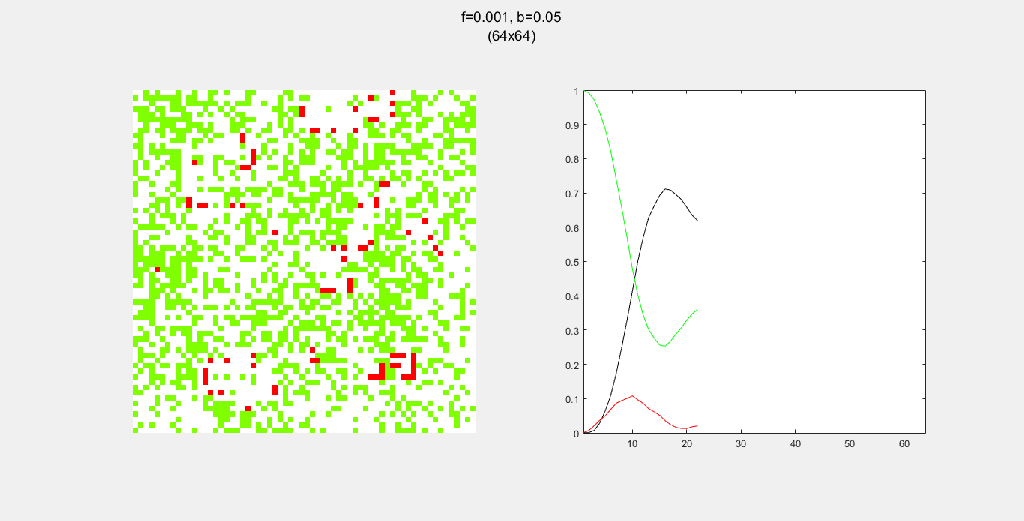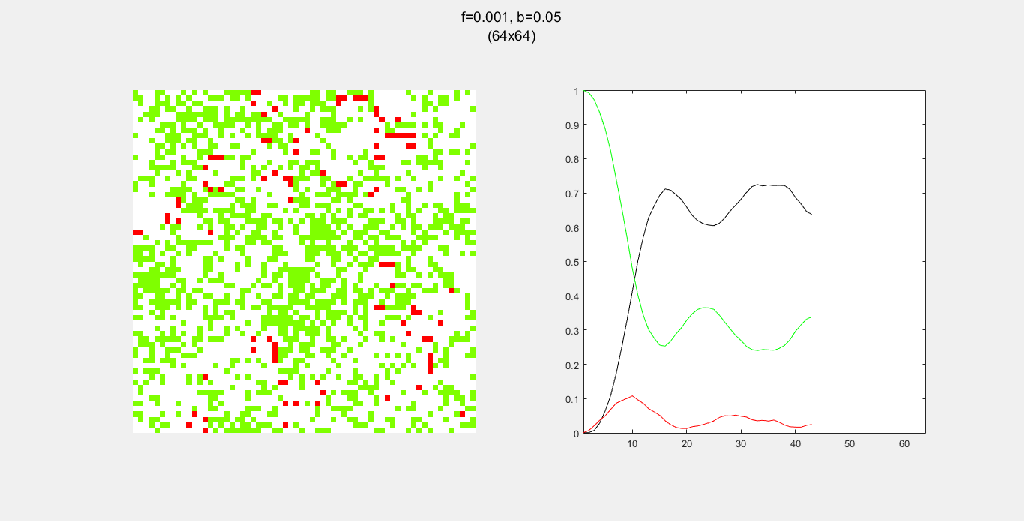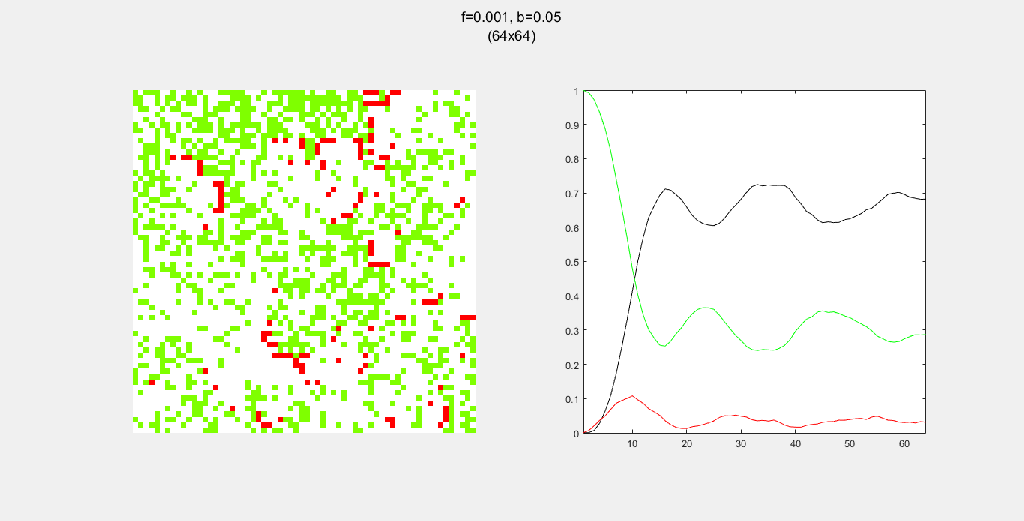
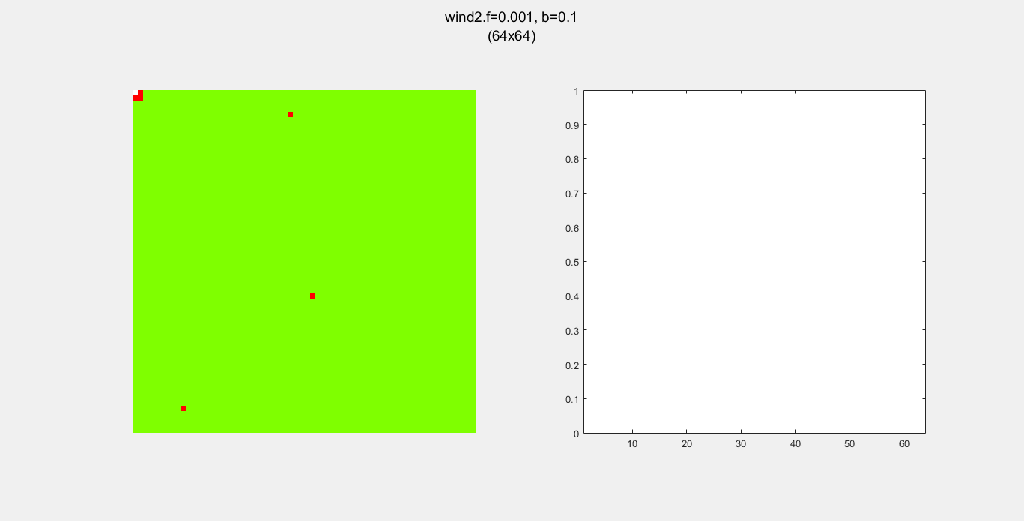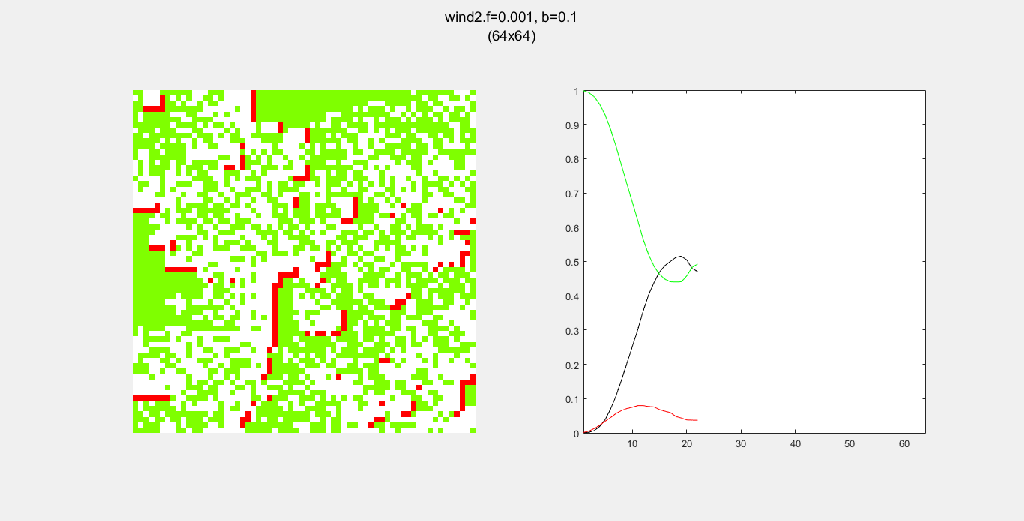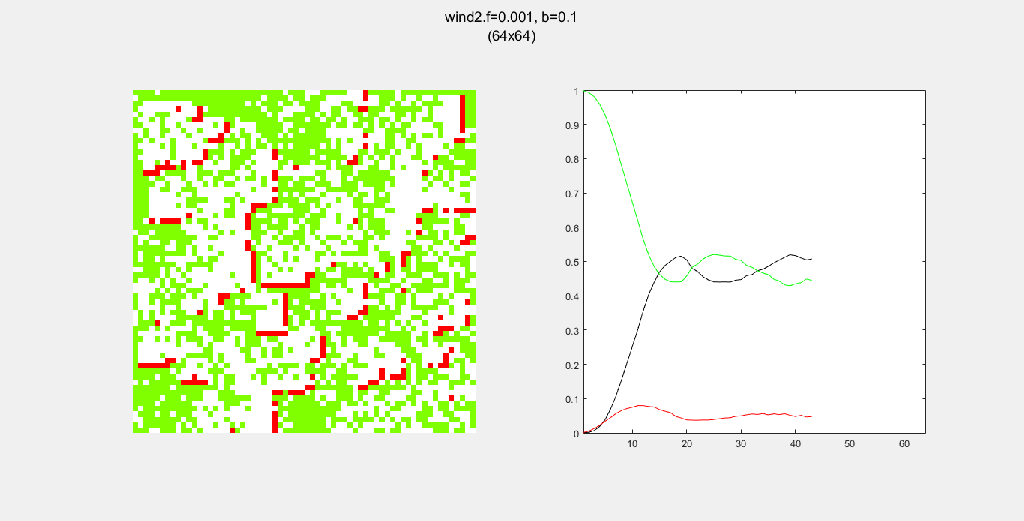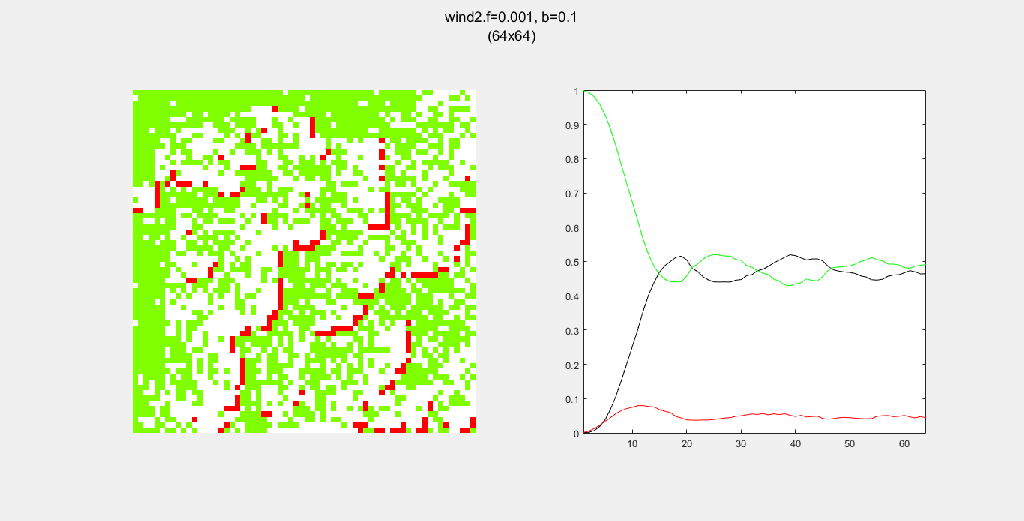
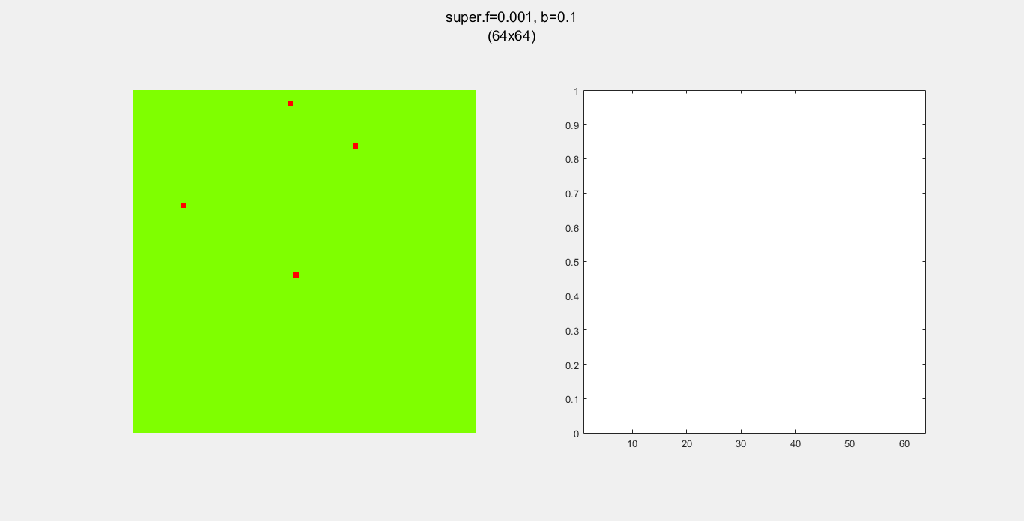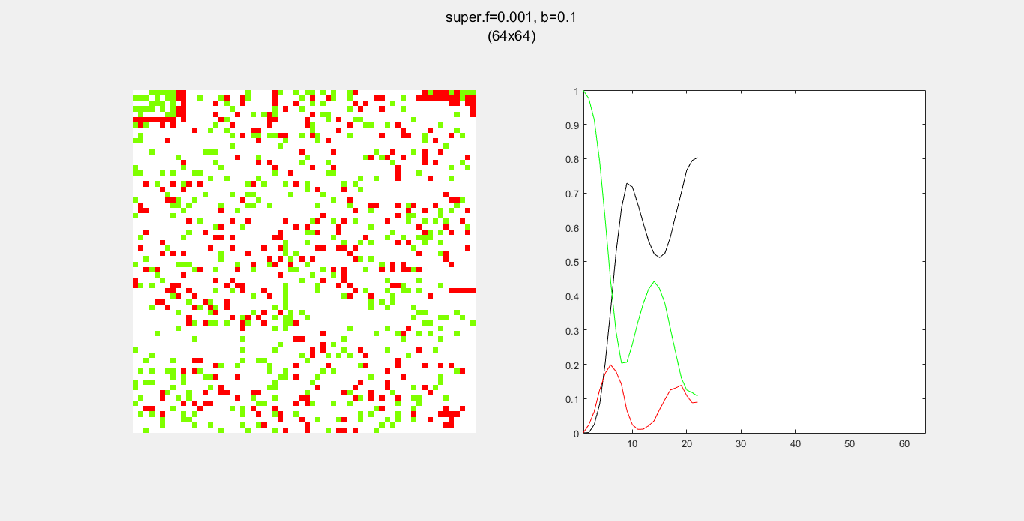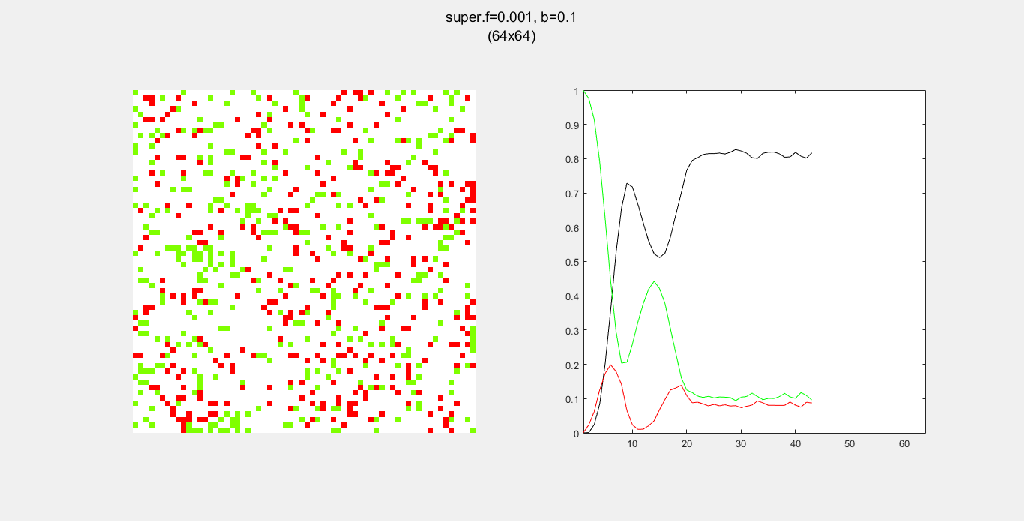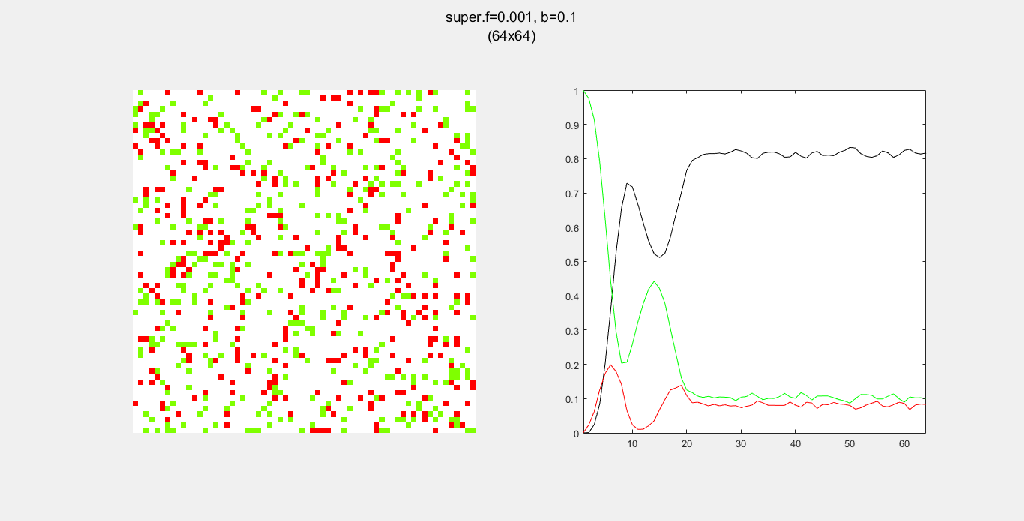
Each gif is composed to two parts: the grid on the left represents the forest, while the plot on the right represents the relative populations for each time step. In the grid, white cells are empty land, green cells are green trees, and red cells are burning trees. In the plot, the black/green/red lines correspond to empty land/green tree/burning tree, respectively.

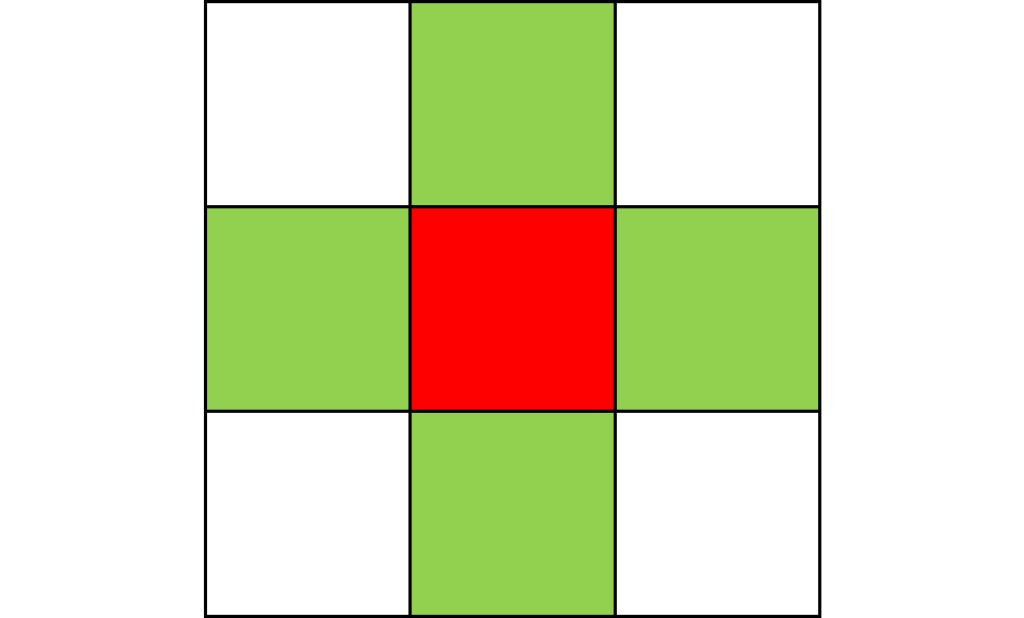
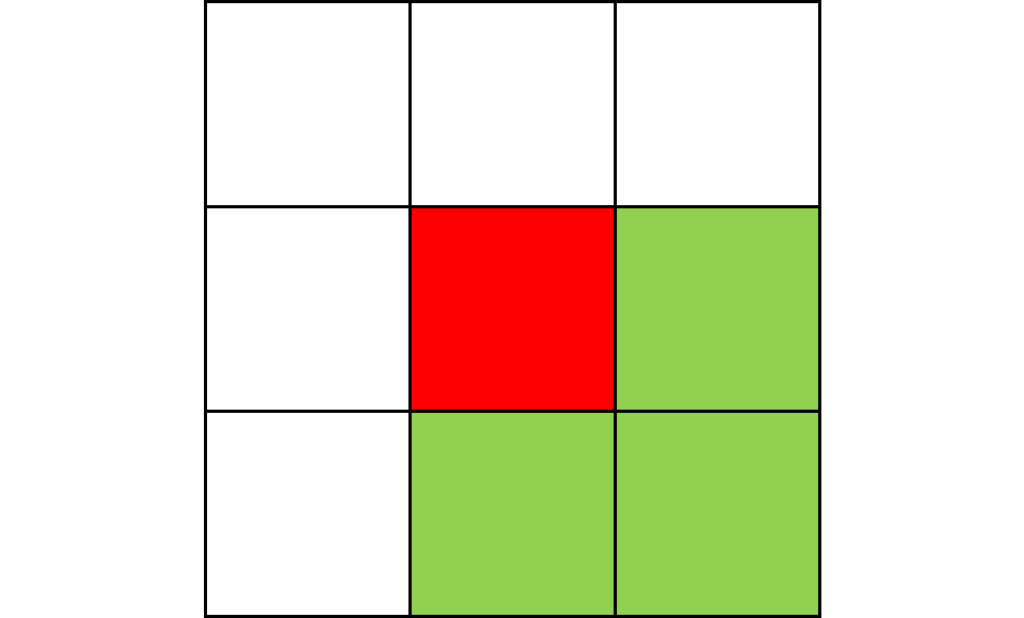
4-way spread pattern

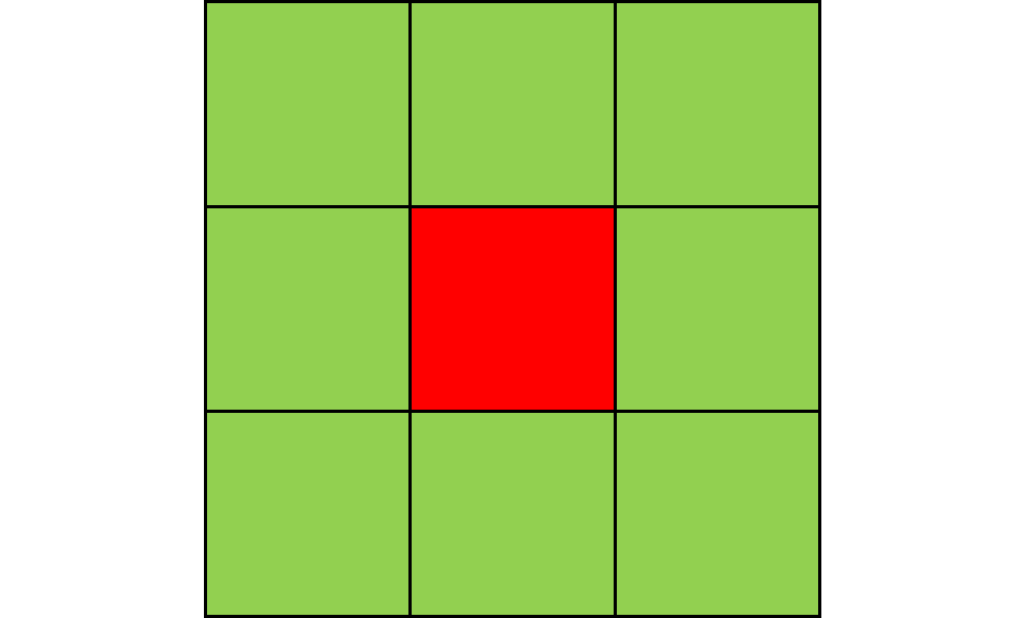
Here, I used a 4-way spread pattern, meaning that any green tree to the left, right, up and down of a burning tree becomes a burning tree at the next time step. The patterns produced spread in a diamond-like pattern. I also noticed that the relative populations appear to oscillate over time. This makes sense to me since more land -> more green trees -> higher chance of a fire starting -> decrease in green trees in the next time step. A higher value of f also increased the initial spread of the fire.

• 

• 

• 

• 

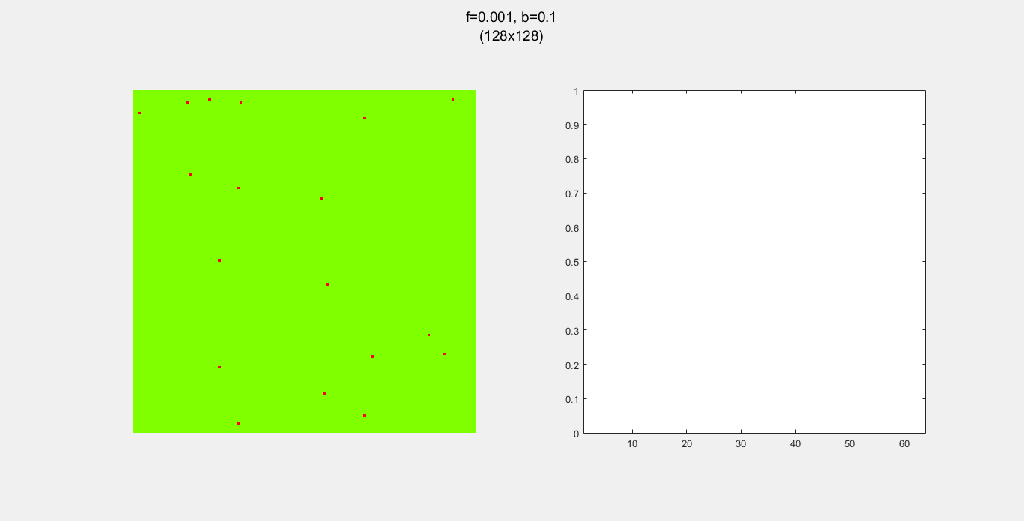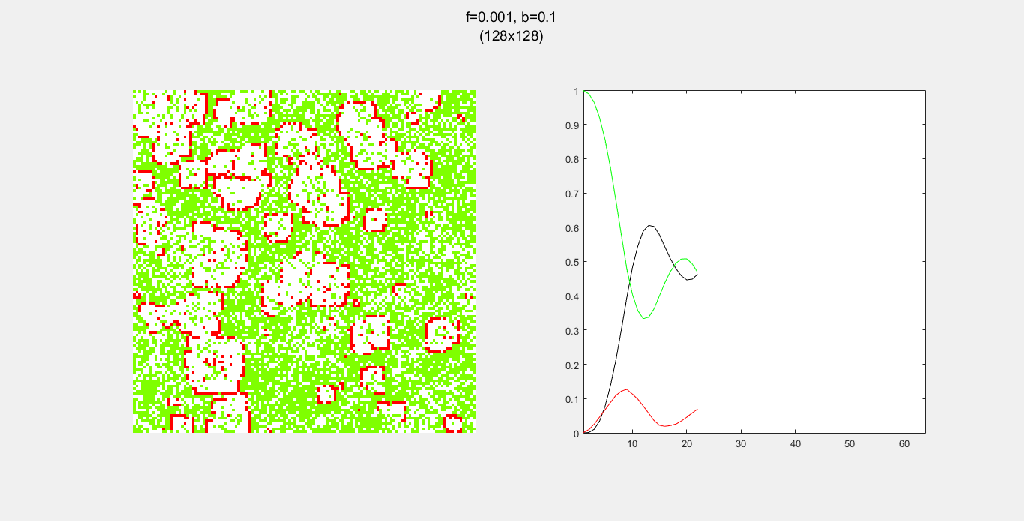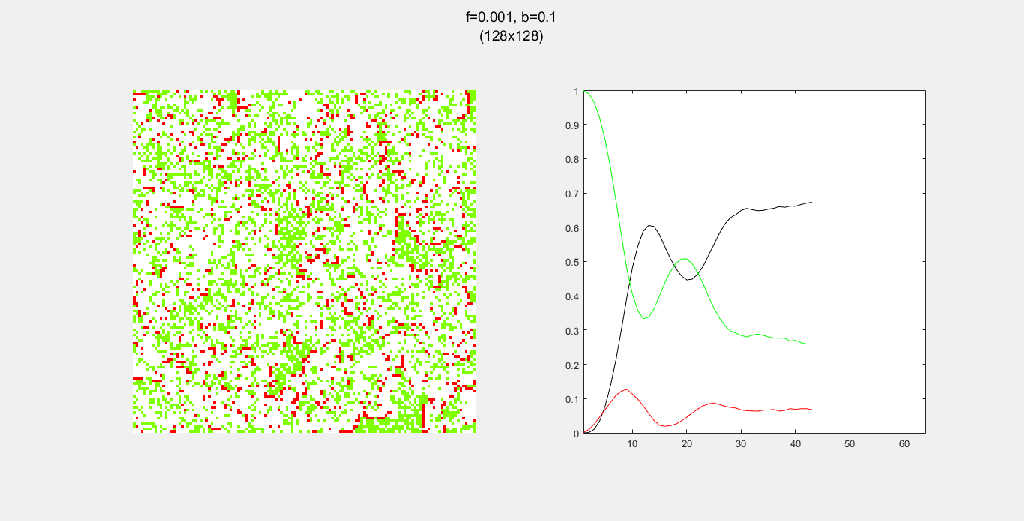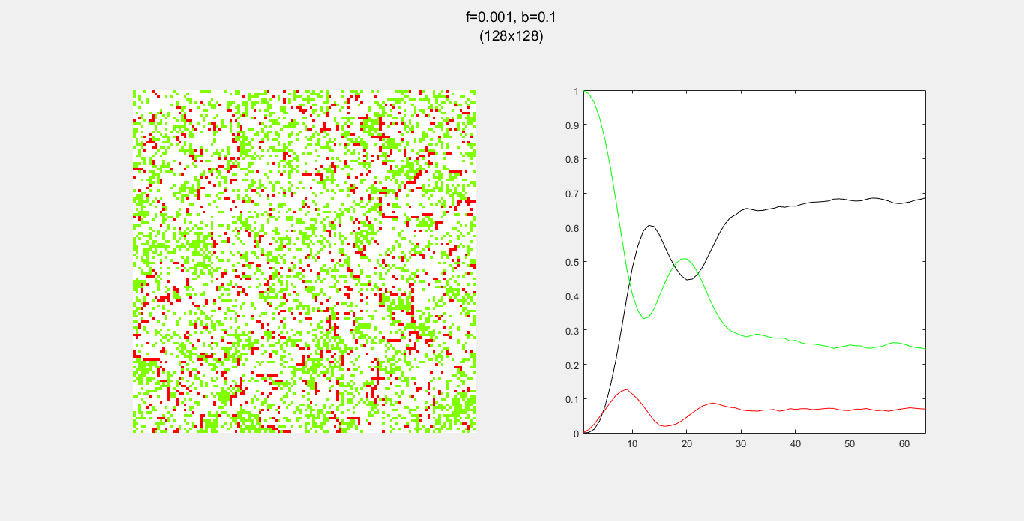
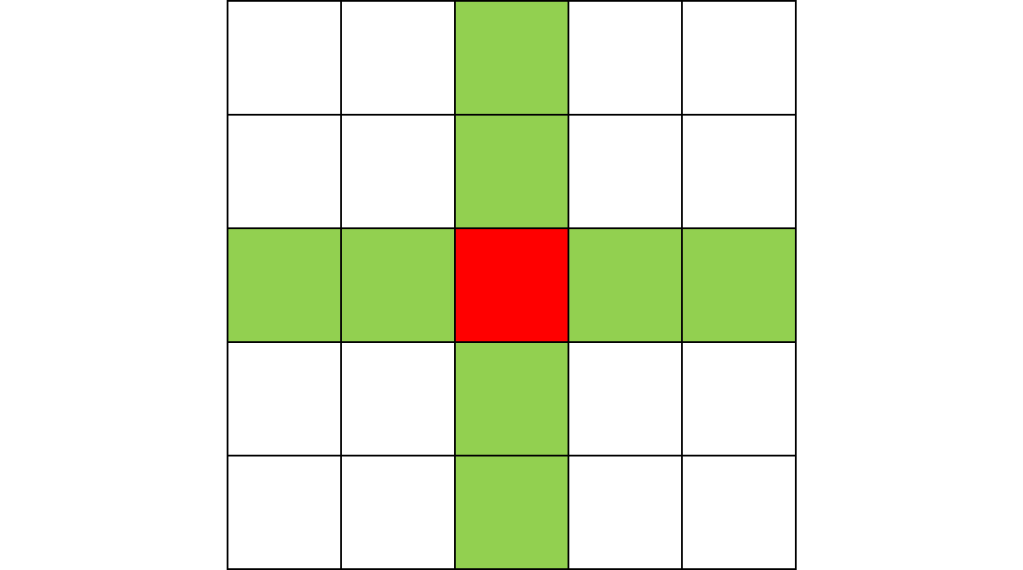
8-way spread pattern

For this one, I used an 8-way spread pattern, which is just like the 4-way spread pattern, but including the diagonals. The three GIFs have the same f and b, for different values of N. As opposed to the 4-way spread pattern, the fire spreads in rectangular patterns.

• 

• 

• 

• 

Playing with fire (probability)

All parameters were held constant here except the fire probability f. Increasing f increased the rate of change/oscillation of the system.

• 

• 

• 

• 

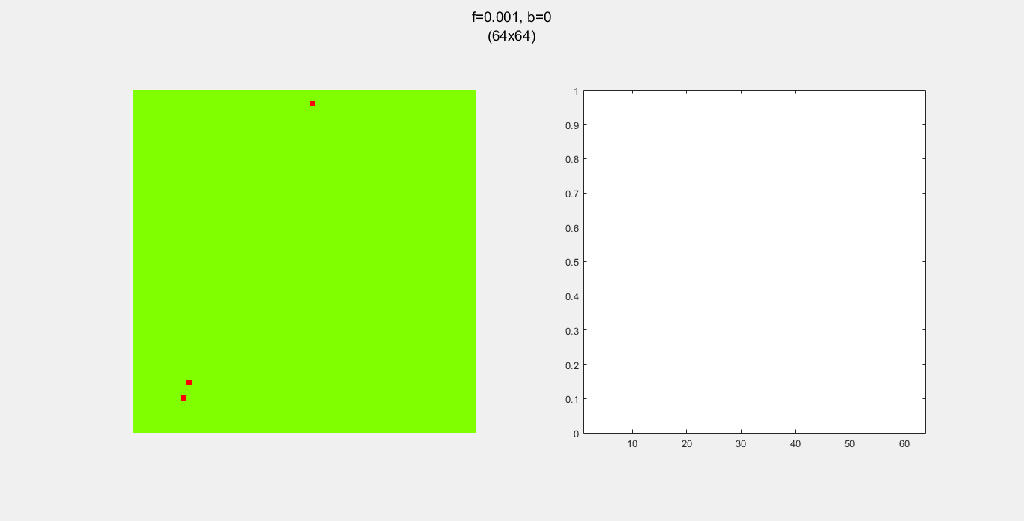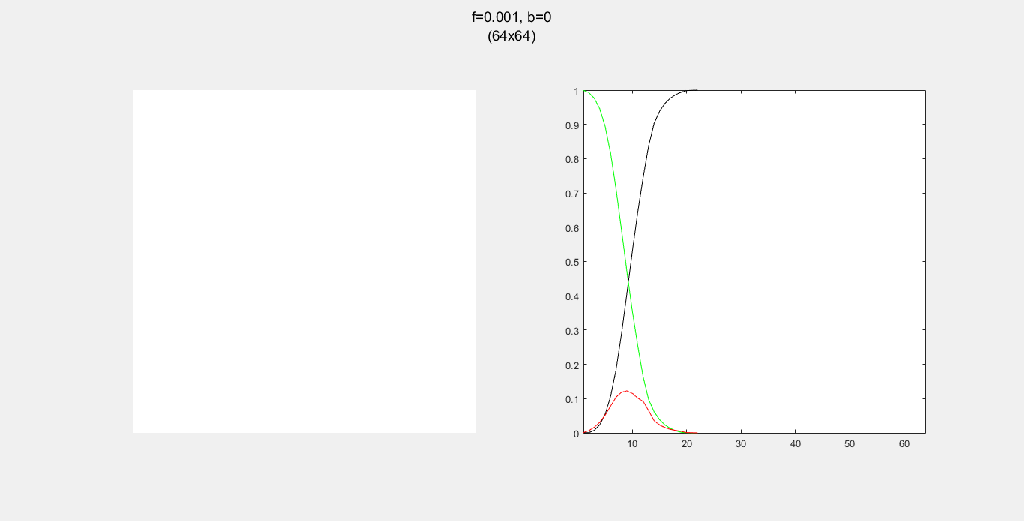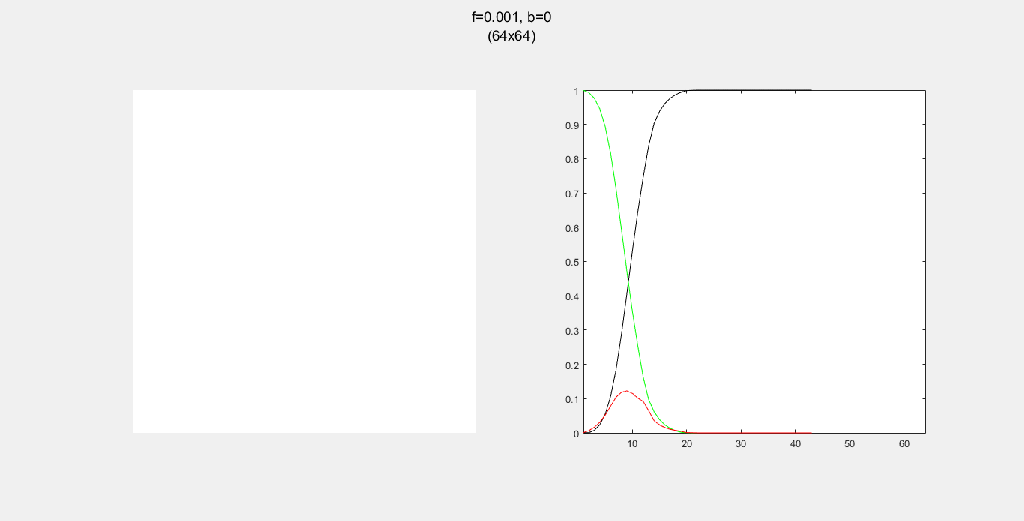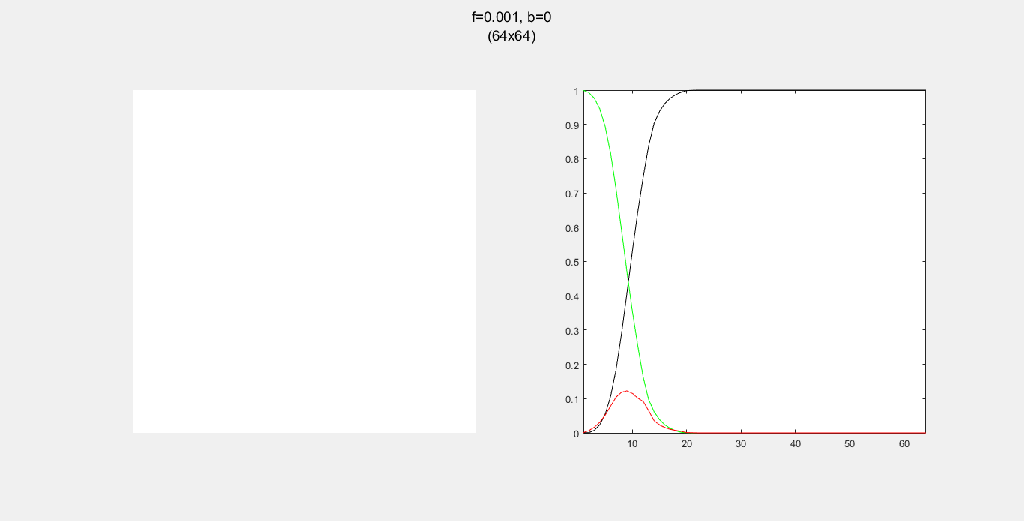
Importance of tree-planting

Setting b to zero quickly leads to a wasteful GIF (since nothing happens after a while). I found it interesting that increasing b led to a more chaotic behavior, since fires have longer lifetimes due to the presence of more trees/fuel.

• 

• 

• 

• 

Miscellanous Patterns

Here, I tried out various spreading patterns. Namely, I used X, wind, bomberman and superspread patterns. The specific spread patterns used and their CA results are found below

• 

• 

• 

• 

• 

• 

• 

• 

Conclusion

With just a few parameter changes, and some simple rules, I was able to produce a great many interesting patterns. I feel as though I have only just skimmed the surface of CA systems. All in all, I had a lot of fun coding this and coming up with the various scenarios.

A possible forward direction for this system is to encode the time it takes for a tree to grow. That is, to delay the “birth” of the trees, as opposed to the instant growth I used for this project. Another would be to include water sources that quench fires that come near them.

Reference

This project on the forest fire was based on the description and suggested parameters found in “Cellular Automata: Simulations Using Matlab” by Stavros Athanassopoulos, Christos Kaklamanis, Gerasimos Kalfoutzos and Evi Papaioannou.

Basic Video Processing

For my final blog of the semester, I’ll aim to apply and synthesize everything I have learned into one exercise – video processing. What is video processing? A video is basically a series of images taken in quick succession. Hence, video processing is just image processing done on multiple time-related images.

In this activity, my partner, Julia Negre, and I aim to verify conservation of energy in a coupled pendulum system (see diagram below).

Schematic diagram of a coupled pendulum

It’s basically two simple pendulums tied to a taut string. It is key that the oscillations be restricted to the axis perpendicular to the pendula’s separation.

More on the Fourier Transforms

Introduction

Due to numerous applications of the Fourier Transform in signal processing (to be discussed soon!), the image processing student should familiarize himself with the general properties of the transformation.

In this blog, the following properties will be discussed: anamorphic, rotational and convolution properties.

Morphological Operations

Introduction

Let’s say you’re given a very messy and clutter picture. For simplicity’s sake, let’s say it’s also a binary image. How would you clean it? Sure, you could go to paint and manually and tediously erase all undesired parts. But what if you had 1,000 of these images? No one would have the patience to manually clean all these images. So what can be done?

Good thing we have – *drumroll please* – Morpological Operations! What are morphological operations? From the name itself, they are processes/operations that work on shapes. One of its applications is in cell-counting, wherein cells are considered as connected blobs, and other shapes, which may be smaller or larger in size, are removed via morphological operations. This blog shall focus on this particular application.

Image Segmentation

Introduction

Greetings!

Image processing is highly useful and efficient when used with a large set of images/data. Applications include the tracking of a region of interest(ROI) throughout these frames. However, if user-intervention is required to locate the ROI, it is very tedious and not at all efficient. Hence, the program must be taught how to automatically detect and isolate the ROI. After isolation, image processing techniques and analysis such as centroid-location and cleaning are more easily applied. This procedure of isolating ROI’s in an image is called Image Segmentation.

In this activity, image segmentation will be performed using color histograms. In essence, this method provides the computer with a reference histogram  or color (chosen by the user) from one frame, with which it uses to locate similar histograms/colors in the succeeding frames. In this work, the technique shall be applied to only one frame (see below).

Test image for image segmentation. Note the two dominant colors (cyan and red).

 

 

Normalized Chromaticity Coordinates (NCC)

The disadvantage of using raw color values(RGB) in image segmentation is that the program becomes very sensitive to changes in lighting/luminance. Hence, ROI’s under different lighting conditions, which usually happens, become difficult to segment.

In order to separate the color from the luminance, normalized chromaticity coordinates(rgb) are used. The following equations convert RGB to rgb:

Credits to Ma’am Jing Soriano for the formulas.

Note that b can be expressed as I – g – r, and hence it is dependent on r and g. Thus, knowledge of r and g is sufficient.

 

Parametric Segmentation

The first technique for image segmentation using histograms is called parametric segmentation, where gaussian curves are fitted to the histograms of the ROI in each of the r and g channels. The gaussian curves represent the probability that a pixel belongs to the ROI. In computer terms, the segmented image is obtained by getting, for each pixel, the probability that it belongs to the ROI, and replacing(backprojecting) that pixel value by this probability. Points with higher probability of belonging to the ROI appear brighter in the segmented image.

The result of using parametric segmentation to isolate the cyan(left) and red(right) colors can be found below. Notice that the results are relatively low contrast, signifying that there is more variation between data points, mainly due to the smooth and slow varying behavior of the gaussian curve fit. Bit depth is also better since no binning occurs since the gaussian curve is fit to the entire data set.

 

Non-parametric segmentation (histogram backprojection)

On the other hand, a similar technique to the one discussed above is called non-parametric segmentation or histogram backprojection. Instead of fitting a gaussian function, the actual value of the histogram is backprojected. That’s it. Sample histograms obtained for the cyan(left) and red(right) ROIs are shown. Note that upper left, lower left and lower right represent pure green, blue and red colors, respectively, while their centroid represents white. Hence, the histograms seem plausible, as cyan lies between green and blue, while the red ROI is isolated to the red corner.

Backprojecting these histogram values to the image results in:

Compared to parametric segmentation, histogram backprojection results in image of higher contrast. This entails better visual inspection, but note that this may also mean that the image is made up of primarily dark and bright portions, and little of the gray portions (due to the binning process of the histogram). However, since histogram backprojection uses the actual histogram values, and not an interpolation, the results are more true to the image.

Conclusion

In conclusion, parametric segmentation can segment images with better bit depth, due to the interpolating nature of the gaussian fit, while histogram backprojection produces higher contrast images due to the binning process.

 

Introduction to the Fourier Transform

Theory behind Fourier Transform

The Fourier Transform (FT) is a linear transformation of f(x) to g(1/x). A common use of this is to convert an image (function of space) into a function of its spatial frequency. While this may useless at the moment, some operations and properties are easier or more obvious when done in the spatial frequency domain, instead of in the usual space domain.

This blog shall cover some basic properties and uses of the Fourier Transform.

Area Estimation

Hello again!

In line with the theme of AP 186 of using digital means to calculate physical and meaningful values, this time, we will be numerically obtaining areas of shapes.

Why is this important? Can’t we just get a ruler and measure the sides? What if the object is so small that 1,000,000 of it can fit between the smallest gradient of your ruler? Or what if the object is irregular and has no exact formula for its area?

This technique can also be used to measure and effectively monitor biological cells, such as to monitor their size and growth. It can also be used in detecting defects in very small objects where only optical techniques, and hence pictures, can detect them.

So how do we numerically calculate the area of any given shape? Well, we will be using Green’s Theorem, which relates a double integral (area) to a line integral(edge). This technique is good for shapes where the edge is very well defined (such as black and white shapes).

For brevity, I will not be including the derivation, but the formula for area using Green’s Theorem is as follows:

Formula for area using Green’s Theorem.

(I did not derive this. Thank you Ma’am Jing Soriano for providing us with the very helpful hand-outs.)

The variables x and y represent the coordinates of the points along the edge of the shape, and are ordered such that they trace a counterclockwise path around the shape. Thus, to get the area, all we need to do is to extract the coordinates of the edge, and order them properly. Sounds easy, right? Maybe. We shall see.

Method

Before I continue, I would again like to acknowledge Ma’am Jing Soriano for providing us with the outline for the method. (We still have to do the coding ourselves, which is also fine.)

1. Convert shape to a binary (i.e. B&W) image to make detecting the edge easier.
2. Extract the edge by using the edge function.  This returns a binary matrix with 0’s and 1’s, where a 1 represents an edge point.
3. Get the coordinates of the edge using find.
4. Convert these coordinates to polar coordinates centered about the centroid of the image.
5. Order the coordinates according to increasing theta.
6. Convert coordinates back to Cartesian coordinates.
7. Calculate area using the formula.
8. Debug your code.
9. Debug again.
10. Celebrate!

Aperture-Generation using MATLAB

Greetings!

For the second activity of Applied Physics 187, we were tasked to generate different grayscale shapes using scilab, octave or MATLAB. I chose MATLAB because I was more familiar with it. In this blog, I’ll explain how my code works, and the shapes they produced.

Initial Parameters

This first piece of code outputs two things: (1) the matrix A filled with 0’s of size (nx, ny) that shall act as the container for the shapes to be produced and (2) the 2D cartesian coordinates from -1 to 1 represented by the X and Y matrices. The vectors x and y represent the x and y coordinate axes. From this, ‘meshgrid’ generates the matrices X and Y, which contain the x and y coordinates for the 2D region (i.e. points off-axis). X and Y make operations over x and y easier. In essence, X andY will determine the conditions for the shapes, while A will be the “canvas” for the shapes. Note that for each point in X or Y, there is a corresponding point in A.

Displaying

The values of A are changed depending on the values of X and Y depending on the desired shape. The next portions describe how to obtain the desired shape in code. The images are then displayed and saved using the following code, where I used ‘export_fig’, a function made and shared by Yair Altman on MATLAB’s File Exchange.

Centered Circle

The first shape is a centered circular aperture. A matrix r is made, which contains the radial distance of the points from (0,0). The next line finds points in A with corresponding r <0.7, and changes their values from 0 to 1. The result is a circle centered at the origin with radius 0.7.

Centered Square

The second shape is a square centered at the origin. I first defined the “apothem”, which is defined as the shortest distance from the center to the side of a regular polygon. It’s kind of like the radius of a circle. Next, I found points whose X and Y coordinates are both less than the apothem, and changed their values in A to 1.

Also, I would like to acknowledge and thank Martin Bartolome for teaching me the usage of the & symbol, which is very useful in shortening codes.

Sine wave along x

In the previous shapes, the binary shapes were produced by making the values of A only 0’s and 1’s. The next shape, the sine wave, is not binary, but has a gradient of values. To do this, the values of X (since we want the sine to  vary along this direction) were inputted into a sine function. The nice thing about using meshgrid to get X and Y is that performing operations is very similar to how we do it by hand, as in this case. The image below is the sine wave viewed from above (looks like a corrugated sheet of metal). The constant multiplied to X controls the frequency and period of the sine wave.

Grating along the x-direction

This shape is very similar to the previous one, but instead of using a sine wave, I used a square wave. The variable m controls how many bars there are.

Annulus

The annulus, or donut, is very similar to the circle. The first step is to make a circle with radius R_out. After that, a circle of radius R_in is deleted (by making the values 0). The result is as follows.

Centered circle with a gaussian gradient

This shape is similar to the centered circle, but instead of having a value of 1, the values of the circle must have a Gaussian distribution. I accomplished this by making bell, a 2D Gaussian bell curve centered at the origin that has the same size as A, which will act as a Gaussian filter. I “filtered” A by performing item-by-item multiplication of A and bell. The parameters amp, center and sigma control the height, location and spread of the gaussian bell curve.

Ellipse (with rotating capabilities)

I enjoyed working out this shape, just because I had to derive the method to rotate the coordinate axes (because I miss Math). Anyway, the variables a and b correspond to the maximum length of the ellipse along the x and y axis, respectively. The x and y axes can be rotated by an angle alpha in the CCW direction using the rotation matrix of cosines and sines, the rotated axes being denoted by Xprime and Yprime. The following images show the ellipse rotated 0, 45 and 90 degrees in the CCW direction.

Cross

Since I had fun rotating the ellipse earlier, I ended up rotating the cross as well. The variable halfwidth, as its name implies, determines half the width of an arm of the cross.  The cross is very similar to the square, but instead of finding points that whose X and Y coordinates are within a certain region, the cross is done by finding points whose X OR Y coordinate is within a certain region. The OR can be done by using | instead of &.

 

 

 

 

 

 

Checkerboard

 

This next shape was not required, but I did it because I found this activity extremely enjoyable, since I love coding. It’s a checkerboard, which is based on the grating. This was accomplished by making two perpendicular gratings (one along x and the other along y), and simply multiplying them term-by-term. The only portions that will remain are the intersections of the two gratings.

For this activity, I’d grade myself a 9/10. For while I enjoyed the activity and finished it relatively early (even having the time to make other shapes), I still made the blog very late.    All in all, I hope this activity will still be done for the next batches.

 

How to digitally scan a line plot (with pictures)

Greetings everyone! My name is Mario and this is my first blog for this website. This blog was created for my Applied Physics 186 course under Dr. Maricor Soriano, and since I haven’t blogged for a while (not since 2011), I’m not really sure if I’m more excited or worried. I’ll just see as I write in this blog.

Our second activity (first for the blog) for the AP 186 course is to digitally scan a line plot. This means that we convert a scan of a line plot, which is composed of pixels, into meaningful physical variables. In other words, we are attempting to retrieve the actual data from a picture of the graph of the data.

I. Finding a hand drawn graph

Since this is only the second activity, we started out with something simple for the plot. The graph should only contain one plot, so as to remove confusion from many plots. Also, the plot must be from an old thesis or dissertation, old enough that the plot is drawn by hand or by an xy-plotter, to  remove the chance that the actual data is easily accessible.

After a quick search in my research laboratory’s library, I found a suitable graph from Ms. Linda Posada’s thesis from 1986, entitled “Modulation Characteristics of Bundle-Integrated-Guide Dynamic Single Mode (BIG-DSM) Semiconductor Lasers.”

Scan of the hand drawn plot as well as the cover of Dr. Linda Posadas’ thesis that it was found in.

II. Conversion Factor

So the problem is – how do we extract or retrieve the actual values of the graph using this scan composed of pixels? In other words, how do we convert the pixel coordinates of a point on the graph into its meaningful physical values? Lucky for us, this graph has equally spaced tick marks; this means that the location of a point measured from the origin of the graph is directly related to the physical value of the point. This would not be the case if the tick marks were in log scale, as the location would be non-linearly related. This key property is depicted below.

The physical values of points A and B can easily be obtained since they are aligned with the tick marks. But what about point C that is located between tick marks? For the case of equally spaced tick marks, it can be inferred that since point C is farther by a factor of 2.5 than A, C is located roughly at 2.5*1 or simply 2.5. But for the case of a log scale, this reasoning would lead to a value of 2.5*10 = 25 if we use A as a reference, or 0.25*100 if we use B. In both cases, we obtain 25, which is obviously wrong since it should be greater than 100.

The method used above is called Ratio and Proportions, and is an excellent way to estimate the physical values of points that are between tick marks. The method works by deriving a conversion factor from a point with known values. In our case, we will derive a conversion factor from pixel coordinates to physical values using the origin and tick marks as reference. We count the number of pixels between all tick marks, and average, to get the conversion factor. This is to be done for the horizontal and vertical tick marks. The respective conversion factors I obtained are roughly 39.5 pixel/horizontal unit and 125.4 pixels/vertical unit. (The decimals are due to the averaging process.)

III. Plot Reconstruction

Equations to convert pixel coordinates to meaningful variables were obtained from the conversion factors (CF). These equations are namely:

x,y are meaningful physical values
subscript ‘pix’ indicates pixel coordinates
subscript ‘o’ indicates origin of the graph

Thus, to reconstruct the graph, I manually determined the pixel coordinates of various points along the plot using MS Paint. I also determined the pixel coordinates of the origin of the graph. Using this data, I used the equations above to determine the meaningful physical values.

To check the validity of the results, I plotted the physical values I calculated and connected the points smoothly using MS Excel. I then used the original image as the chart background and adjusted the size. A nice fit between the reconstructed graph and the original image means that the physical values obtained are accurate. Below is the picture of the overlaid graphs.

Calculated physical values overlaid the image.

A good fit is observed, showing that the reconstruction is valid.

IV. Limitations of the Ratio and Proportion technique

As I performed the activity, I noticed some limitations. Firstly, it is very important that the axes of the graph are as horizontal and vertical as possible (i.e. aligned with the edges of the image), so as to simplify the conversion equation. It can still be compensated however by transforming to a rotated pixel coordinate system.

Secondly, it is very important that the tick marks are equally spaced. This simplifies the conversion into just a scaling problem, which is easily performed using just excel.

Lastly, a better fit is obtained if the pixel coordinates obtained from the curve are not equally spaced. That is, the sharper the curve, or the more rapidly the curve changes, the more points must be taken. Taking equally spaced points would result in the following reconstruction:

It can be observed that the reconstruction is somewhat lacking for the sharp curves.

Thus, to get a good reconstruction, great care must be taken in making the axes square with the image, and many points must be taken to get a good reconstruction. All in all, the work is quite tedious, but I still had fun in doing this activity. Would be nice to semi-automate the process though.